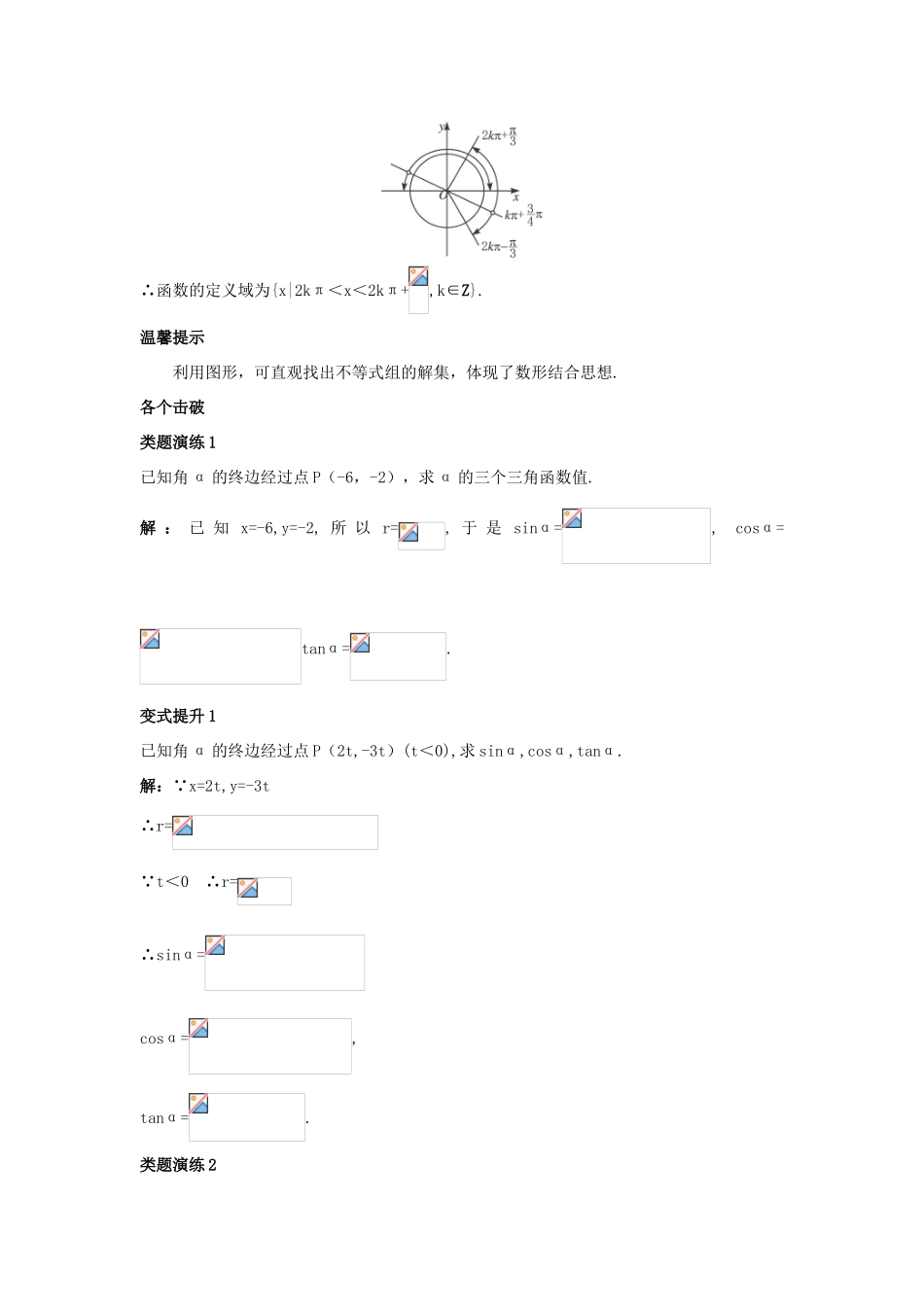
1.2.1 任意角的三角函数课堂导学三点剖析1.任意角的正弦、余弦、正切的定义【例 1】有下列命题,其中正确的命题的个数是( )① 终边相同的角的同名三角函数的值相同② 终边不同的角的同名三角函数的值不等③ 若 sinα>0,则 α 是第一、二象限的角④ 若 α 是第二象限的角,且 P(x,y)是其终边上一点,则 cosα=A.1 B.2 C.3 D.4思路分析:运用概念判断.解析:由任意角三角函数定义知①正确;对②,我们举出反例 sin=sin;对③,可指出 sin>0,但不是第一、二象限的角;对④,应是 cosα=.综上选 A.答案:A温馨提示 要准确地理解任意角的三角函数定义,可与三角函数线结合记忆.2.角、实数和三角函数值之间的对应关系【例 2】 判断下列各式的符号.(1)tan250°·cos(-350°);(2)sin151°cos230°;(3)sin3cos4tan5;(4)sin(cosθ)·cos(sinθ)(θ 是第二象限角).思路分析:本题主要考查三角函数的符号.角度确定了,所在的象限也就确定了.三角函数的符号也就确定了.进一步再确定各式的符号.对于(4),视 sinθ、cosθ 为弧度数.解:(1) tan250°>0,cos(-350°)>0,∴tan250°·cos(-350°)>0.(2) sin151°>0,cos230°<0,∴sin151°·cos230°<0.(3) <3<π,π<4<,<5<2π,∴sin3>0,cos4<0,tan5<0,∴sin3·cos4·tan5>0.(4) θ 是第二象限角,∴0<sinθ<1<,∴cos(sinθ)>0.同理,-<-1<cosθ<0,∴sin(cosθ)<0,故 sin(cosθ)·cos(sinθ)<0.温馨提示 (1)判断各三角函数值的符号,须判断角所在的象限.(2)sinθ 既表示角 θ 的正弦值,同时也可以表示[-1,1]上的一个角的弧度数.(3)中解题的关键是将 cosθ、sinθ 视为角的弧度数.【例 3】求函数 y=的定义域.思路分析:运用等价及集合的思想.解:只需满足条件∴函数的定义域为{x|2kπ<x<2kπ+,k∈Z}.温馨提示 利用图形,可直观找出不等式组的解集,体现了数形结合思想.各个击破类题演练 1已知角 α 的终边经过点 P(-6,-2),求 α 的三个三角函数值.解 : 已 知 x=-6,y=-2, 所 以 r=, 于 是 sinα=, cosα=tanα=.变式提升 1已知角 α 的终边经过点 P(2t,-3t)(t<0),求 sinα,cosα,tanα.解: x=2t,y=-3t∴r= t<0 ∴r=∴sinα=cosα=,tanα=.类题演练 2判断下列各式的符号(1)sin105°·cos230°;(2)sinπ·tanπ;(3)cos6·tan 6;(4)sin4·tan().解:(1) 105°、230°分别为第二、...