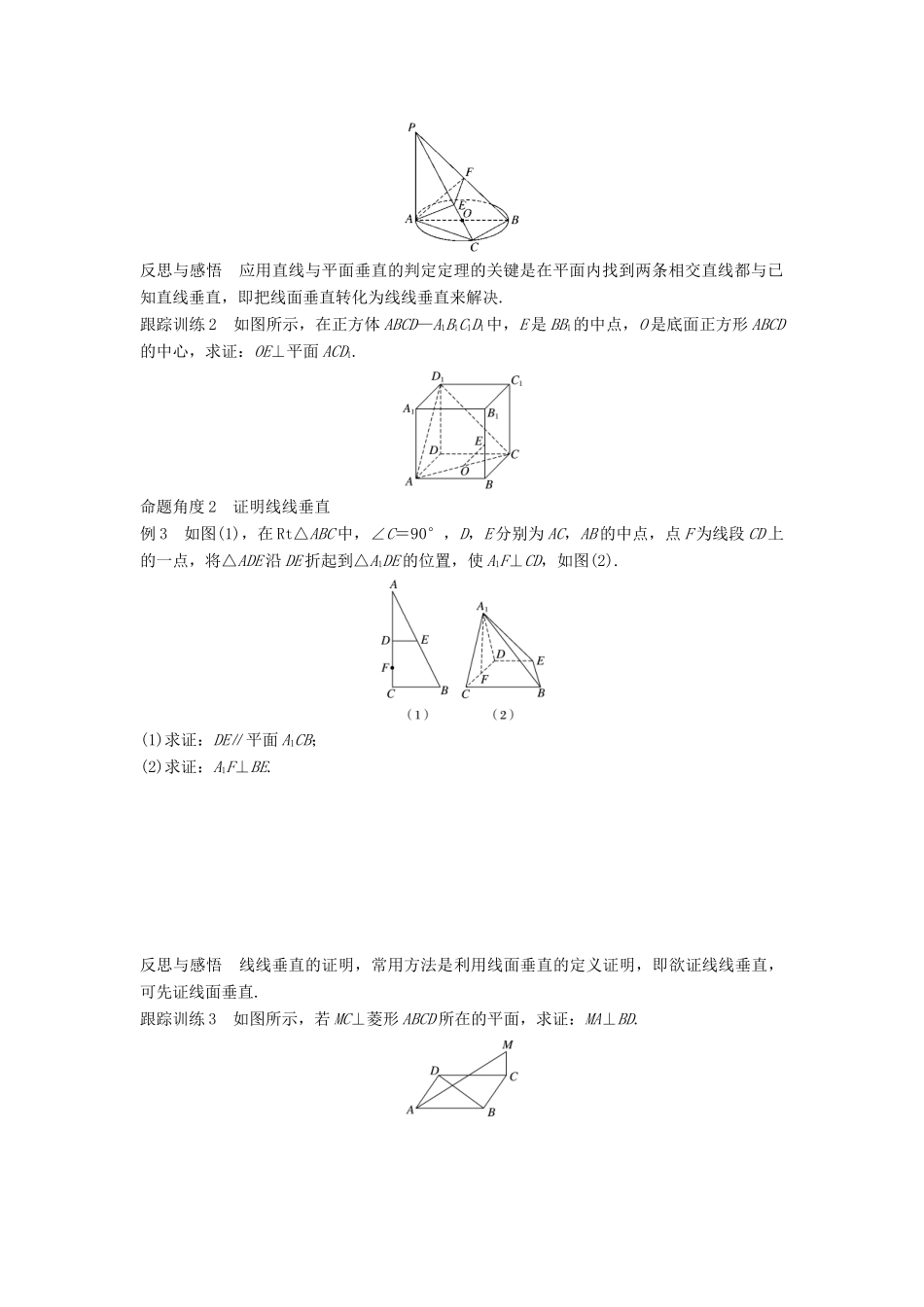
第 3 课时 直线与平面垂直的判定学习目标 1.理解直线与平面垂直的定义.2.掌握直线与平面垂直的判定定理,并能灵活应用判定定理证明直线与平面垂直.知识点一 直线与平面垂直的定义思考 在阳光下观察直立于地面的旗杆及它在地面上的影子,随着时间的变化,影子的位置在移动,在各个时刻旗杆所在的直线与其影子所在的直线的夹角是否发生变化,为多少?梳理定义如果一条直线 a 与一个平面 α 内的________直线都垂直,我们就说直线 a 与平面 α 互相垂直记法有关概念线 a 叫做平面 α 的______,平面 α 叫做直线 a 的______,垂线和平面的交点 P 称为______图示画法画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直知识点二 直线和平面垂直的判定定理 将一块三角形纸片 ABC 沿折痕 AD 折起,将翻折后的纸片竖起放置在桌面上(BD,DC 与桌面接触).观察折痕 AD 与桌面的位置关系.思考 1 折痕 AD 与桌面一定垂直吗? 思考 2 当折痕 AD 满足什么条件时,AD 与桌面垂直? 梳理文字如果一条直线和一个平面内的_________垂直,那么这条直线垂直于这个平面符号语言a⊥m,a⊥n,m⊂α,n⊂α,______=A⇒a⊥α图形语言类型一 线面垂直的定义例 1 下列命题中,正确的序号是________.① 若直线 l 与平面 α 内的无数条直线垂直,则 l⊥α;② 若直线 l 与平面 α 内的一条直线垂直,则 l⊥α;③ 若直线 l 不垂直于平面 α,则 α 内没有与 l 垂直的直线;④ 若直线 l 不垂直于平面 α,则 α 内也可以有无数条直线与 l 垂直;⑤ 过一点和已知平面垂直的直线有且只有一条.反思与感悟 (1)直线和平面垂直的定义是描述性定义,对直线的任意性要注意理解.实际上,“任意一条”与“所有”表达相同的含义.当直线与平面垂直时,该直线就垂直于这个平面内的任何直线.由此可知,如果一条直线与一个平面内的一条直线不垂直,那么这条直线就一定不与这个平面垂直.(2)由定义可得线面垂直⇒线线垂直,即若 a⊥α,b⊂α,则 a⊥b.跟踪训练 1 设 l,m 是两条不同的直线,α 是一个平面,则下列命题正确的是________.(填序号)① 若 l⊥m,m⊂α,则 l⊥α;② 若 l⊥α,l∥m,则 m⊥α;③ 若 l∥α,m⊂α,则 l∥m;④ 若 l∥α,m∥α,则 l∥m.类型二 线面垂直的判定定理的应用命题角度 1 证明线面垂直例 2 如图所示,已知 PA 垂直于⊙O 所...