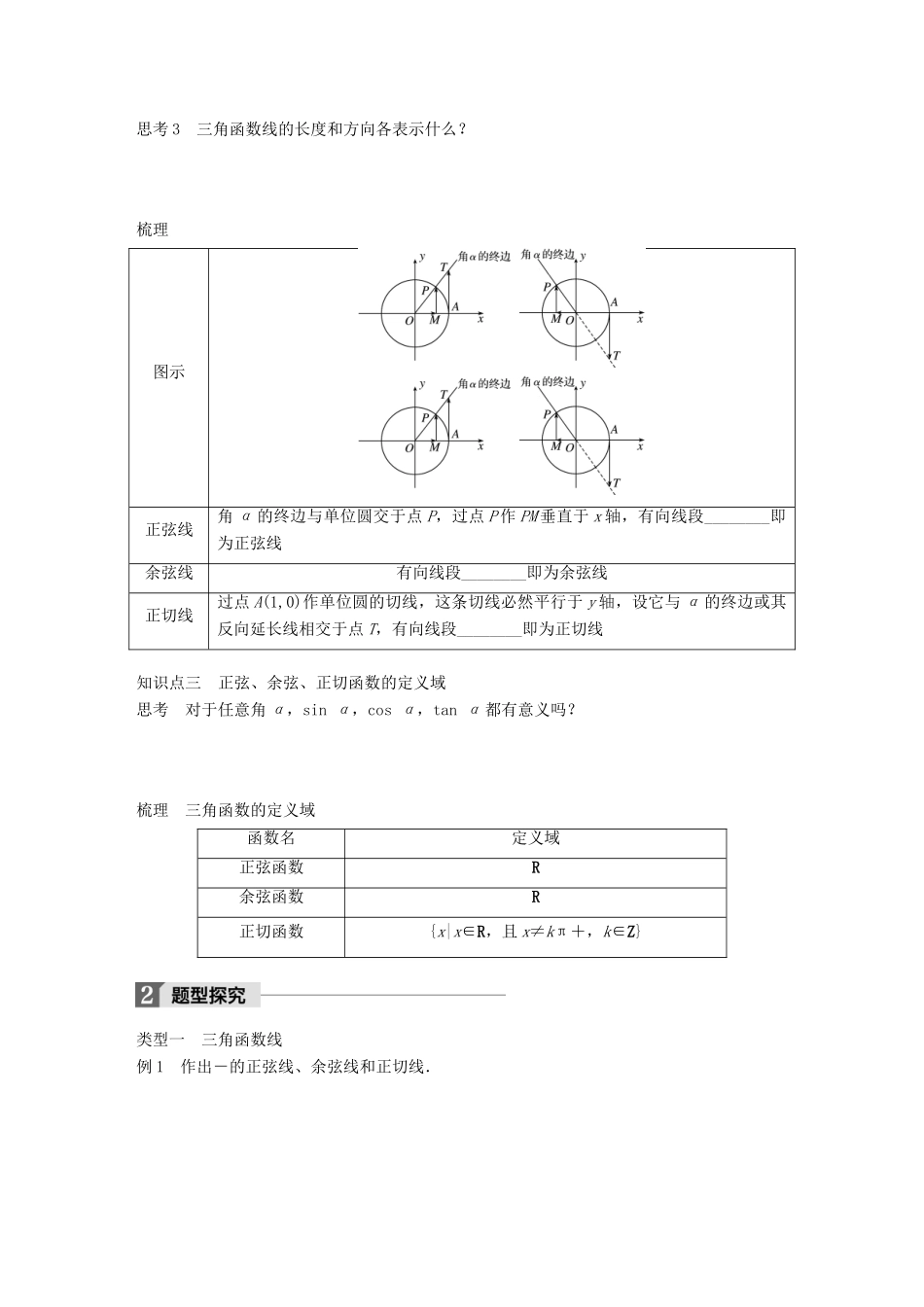
第 2 课时 三角函数线学习目标 1.掌握正弦、余弦、正切函数的定义域.2.了解三角函数线的意义,能用三角函数线表示一个角的正弦、余弦和正切.3.能利用三角函数线解决一些简单的三角函数问题.知识点一 有向线段思考 1 比如你从学校走到家和你从家走到学校,效果一样吗? 思考 2 如果你觉得效果不同,怎样直观的表示更好? 梳理 有向线段(1)有向线段:规定了________(即规定了起点和终点)的线段称为有向线段.(2)有向直线:规定了正方向的直线称为有向直线.(3)有向线段的数量:根据有向线段 AB 与有向直线 l 的方向相同或相反,分别把它的长度添上______或______,这样所得的数,叫做有向线段的数量,记为 AB.(4)单位圆:圆心在________,半径等于____________的圆.知识点二 三角函数线思考 1 在平面直角坐标系中,任意角 α 的终边与单位圆交于点 P,过点 P 作 PM⊥x 轴,过点 A(1,0)作单位圆的切线,交 α 的终边或其反向延长线于点 T,如图所示,结合三角函数的定义,你能得到 sin α,cos α,tan α 与 MP,OM,AT 的关系吗? 思考 2 三角函数线的方向是如何规定的? 思考 3 三角函数线的长度和方向各表示什么? 梳理 图示正弦线角 α 的终边与单位圆交于点 P,过点 P 作 PM 垂直于 x 轴,有向线段________即为正弦线余弦线有向线段________即为余弦线正切线过点 A(1,0)作单位圆的切线,这条切线必然平行于 y 轴,设它与 α 的终边或其反向延长线相交于点 T,有向线段________即为正切线知识点三 正弦、余弦、正切函数的定义域思考 对于任意角 α,sin α,cos α,tan α 都有意义吗? 梳理 三角函数的定义域函数名定义域正弦函数R余弦函数R正切函数{x|x∈R,且 x≠kπ+,k∈Z}类型一 三角函数线例 1 作出-的正弦线、余弦线和正切线. 反思与感悟 (1)作正弦线、余弦线时,首先找到角的终边与单位圆的交点,然后过此交点作 x 轴的垂线,得到垂足,从而得到正弦线和余弦线.(2)作正切线时,应从点 A(1,0)引单位圆的切线交角的终边或终边的反向延长线于一点 T,即可得到正切线 AT.跟踪训练 1 在单位圆中画出满足 sin α=的角 α 的终边,并求角 α 的取值集合. 类型二 利用三角函数线比较大小例 2 利用三角函数线比较 sin 和 sin,cos 和 cos,tan 和 tan 的大小. 反思与感悟 利用三角函数线比较三角函数值的大小时,一般分三步...