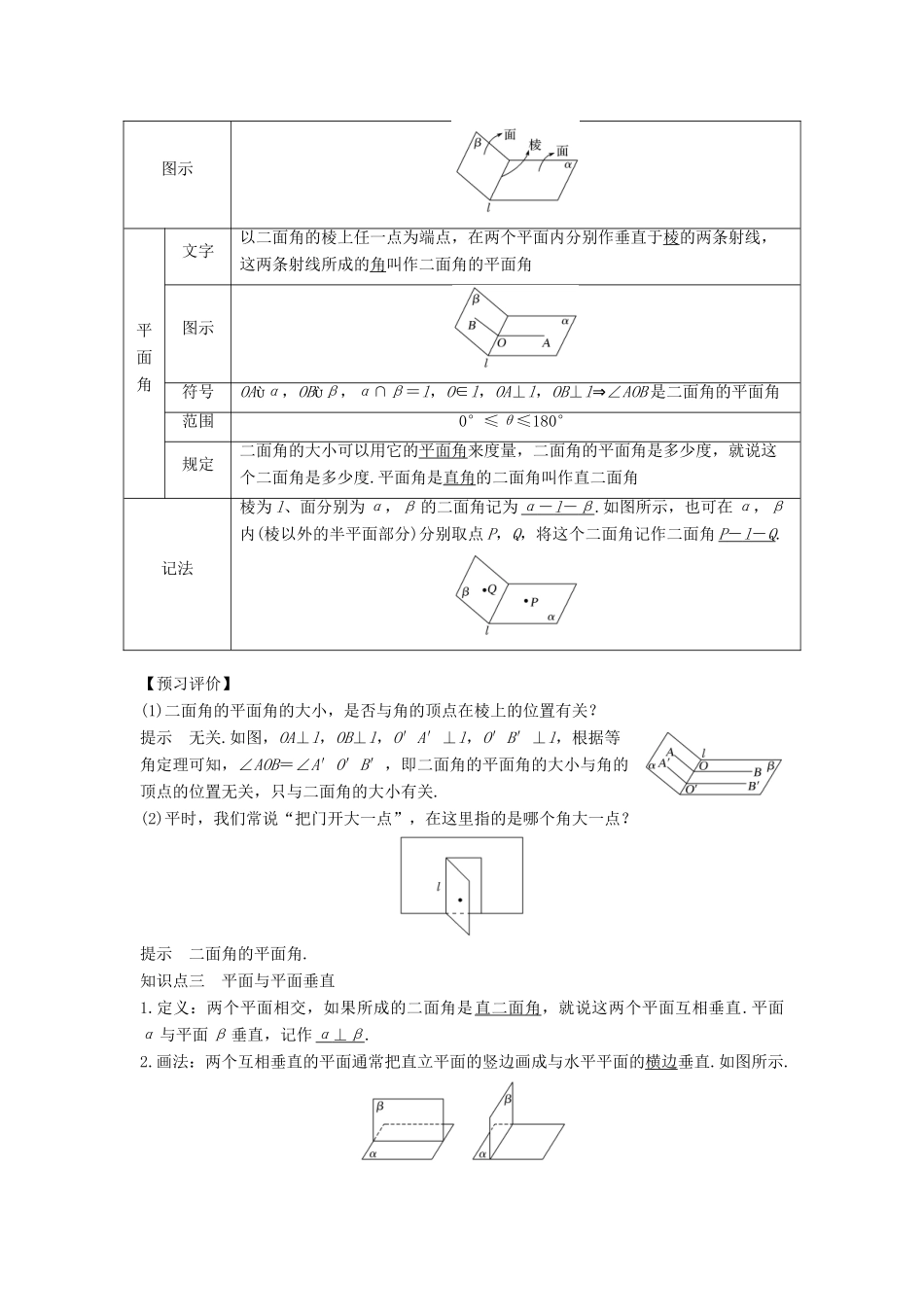
6.1 垂直关系的判定学习目标 1.掌握直线与平面垂直的判定定理(重点);2.理解二面角的有关概念,会求简单的二面角的大小(重、难点);3.掌握两平面垂直的判定定理(重点).知识点一 直线与平面垂直的判定定理文字语言如果一条直线和一个平面内的两条相交直线都垂直,那么该直线与此平面垂直符号语言l⊥a,l⊥b,aα,bα,a ∩ b = P ⇒l⊥α图形语言【预习评价】(1)线面垂直判定定理中,平面内两条相交直线和已知直线 l 必须有公共点吗?提示 用线面垂直判定定理判定直线与平面垂直,取决于在这个平面内能否找出两条相交直线和已知直线垂直,至于这两条相交直线是否和已知直线有公共点,则是无关紧要的.(2)在阳光下观察直立于地面的旗杆及它在地面上的影子,随着时间的变化,影子的位置在移动,在各个时刻旗杆所在的直线与其影子所在的直线夹角是否发生变化,为多少?提示 不变,90°.(3)下列说法中正确的个数是( )① 若直线 l 与平面 α 内一条直线垂直,则 l⊥α;② 若直线 l 与平面 α 内两条直线垂直,则 l⊥α;③ 若直线 l 与平面 α 内两条相交直线垂直,则 l⊥α;④ 若直线 l 与平面 α 内任意一条直线垂直,则 l⊥α;⑤ 若直线 l 与平面 α 内无数条直线垂直,则 l⊥α.A.1 B.2 C.3 D.4解析 对①②⑤,由于缺少“相交”二字,不能断定该直线与平面垂直,该直线与平面可能平行,可能斜交,也可能在平面内,所以是错误的.正确的是③④,故选 B.答案 B知识点二 二面角概念一个平面内的一条直线,把这个平面分成两部分,其中的每一部分都叫作半平面.从一条直线出发的两个半平面所组成的图形叫作二面角.这条直线叫作二面角的棱,这两个半平面叫作二面角的面.图示平面角文字以二面角的棱上任一点为端点,在两个平面内分别作垂直于棱的两条射线,这两条射线所成的角叫作二面角的平面角图示符号OAα,OBβ,α∩β=l,O∈l,OA⊥l,OB⊥l⇒∠AOB 是二面角的平面角范围0°≤θ≤180°规定二面角的大小可以用它的平面角来度量,二面角的平面角是多少度,就说这个二面角是多少度.平面角是直角的二面角叫作直二面角记法棱为 l、面分别为 α,β 的二面角记为 α - l - β .如图所示,也可在 α,β内(棱以外的半平面部分)分别取点 P,Q,将这个二面角记作二面角 P - l - Q .【预习评价】(1)二面角的平面角的大小,是否与角的顶点在棱上的位置有关?提示 无关.如...