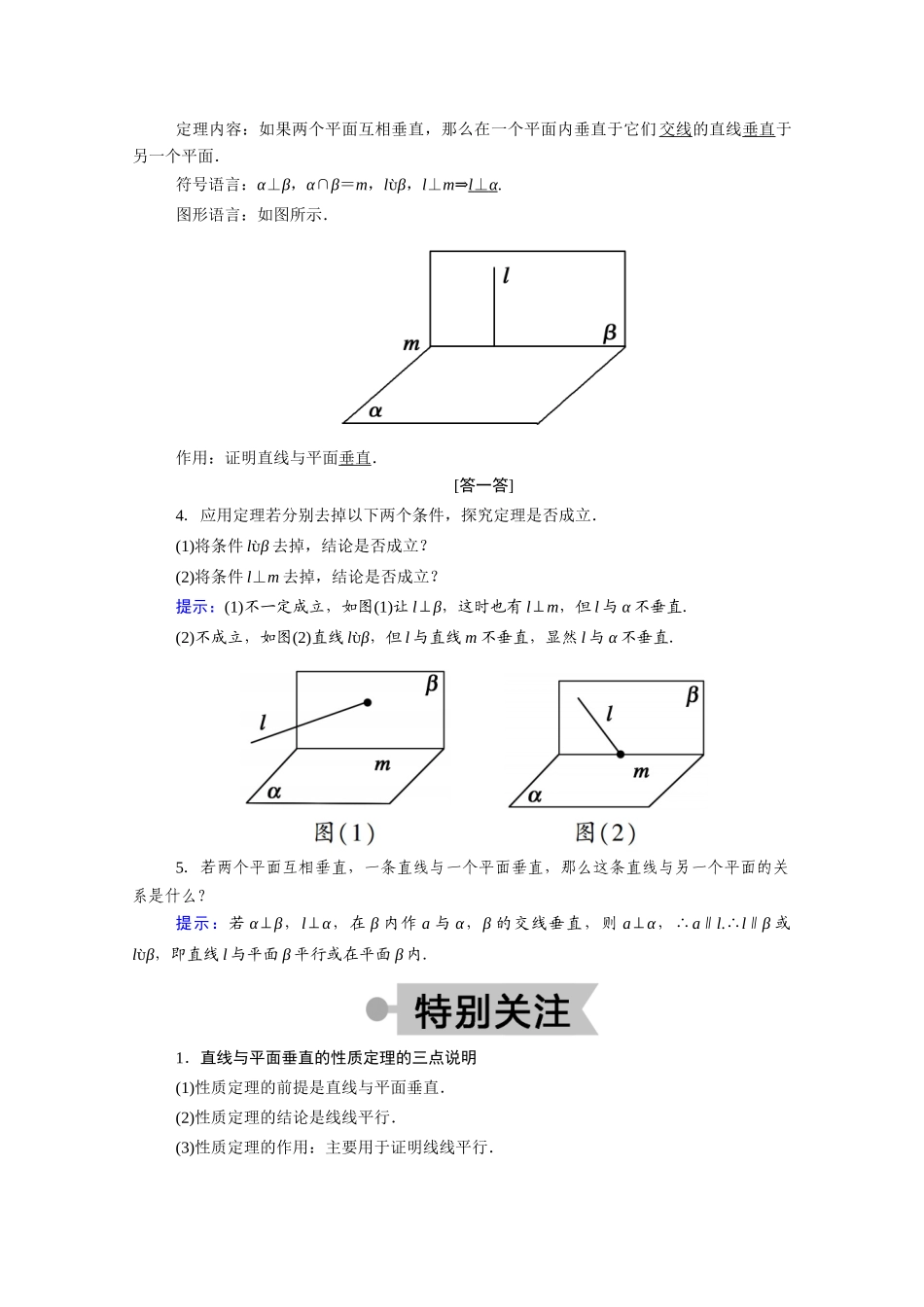
6.2 垂直关系的性质知识点一 直线与平面垂直的性质定理 [填一填]定理内容:如果两条直线同垂直于一个平面,那么这两条直线平行.符号语言:a⊥α,b⊥α⇒a ∥ b .图形语言:如图所示.作用:证明两直线平行.[答一答]1.两条平行线中的一条垂直于一个平面,另一条也垂直于这个平面吗?提示:垂直.因为两条平行线中的一条垂直于这个平面,所以这条直线垂直于平面内的两条相交直线,所以另一条直线也垂直于这两条相交直线,故另一条也垂直于这个平面.2.分别垂直于两个平行平面的两条直线是否平行?提示:平行.因为一条直线垂直于一个平面,那么这条直线垂直于这个平面的平行平面,所以这两条直线垂直于同一个平面,所以这两条直线平行.3.垂直于同一条直线的两平面平行吗?提示:平行.如图,过直线 l 作两个平面,分别与两个平面 α,β 相交于 a,a′,b,b′, l⊥α,∴l⊥a,l⊥b. l⊥β,∴l⊥a′,l⊥b′.∴a∥a′,b∥b′.又 a 与 b 相交,a′与 b′相交,∴α∥β.∴垂直于同一条直线的两个平面平行.知识点二 平面与平面垂直的性质定理 [填一填]定理内容:如果两个平面互相垂直,那么在一个平面内垂直于它们 交线的直线垂直于另一个平面.符号语言:α⊥β,α∩β=m,lβ,l⊥m⇒l ⊥ α .图形语言:如图所示.作用:证明直线与平面垂直.[答一答]4.应用定理若分别去掉以下两个条件,探究定理是否成立.(1)将条件 lβ 去掉,结论是否成立?(2)将条件 l⊥m 去掉,结论是否成立?提示:(1)不一定成立,如图(1)让 l⊥β,这时也有 l⊥m,但 l 与 α 不垂直.(2)不成立,如图(2)直线 lβ,但 l 与直线 m 不垂直,显然 l 与 α 不垂直.5.若两个平面互相垂直,一条直线与一个平面垂直,那么这条直线与另一个平面的关系是什么?提示:若 α⊥β,l⊥α,在 β 内作 a 与 α,β 的交线垂直,则 a⊥α,∴a∥l.∴l∥β 或lβ,即直线 l 与平面 β 平行或在平面 β 内.1.直线与平面垂直的性质定理的三点说明(1)性质定理的前提是直线与平面垂直.(2)性质定理的结论是线线平行.(3)性质定理的作用:主要用于证明线线平行.2.直线与平面垂直的常见性质(1)过一点有且只有一条直线和已知平面垂直.(2)过一点有且只有一个平面和已知直线垂直.(3)垂直于同一直线的两个平面平行.3.平面与平面垂直的性质定理的关注点(1)性质定理成立要有两个条件:一是线在面内,二是线...