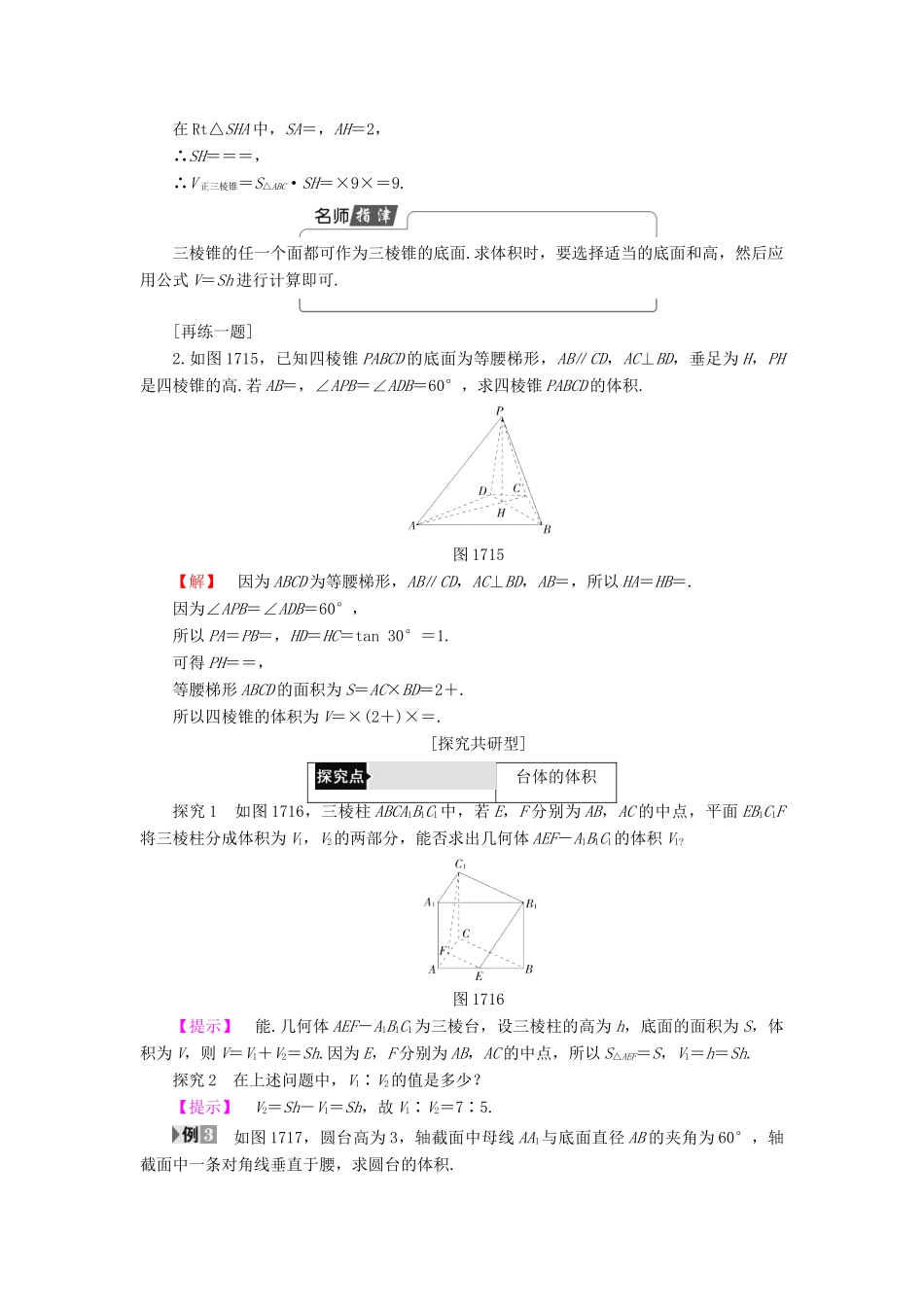
7.2 柱、锥、台的体积1.理解棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积公式.(重点)2.熟练运用体积公式求多面体和旋转体的体积.(难点)[基础·初探]教材整理 柱、锥、台的体积阅读教材 P46“练习”以下至 P48“例 5”以上部分,完成下列问题.几何体体积说明柱体V 柱体=ShS 为柱体的底面积,h 为柱体的高锥体V 锥体=ShS 为锥体的底面积,h 为锥体的高台体V 台体=(S 上++S 下)·hS 上, S 下分别为台体的上、下底面积,h为高直角三角形两直角边 AB=3,AC=4,以 AB 为轴旋转所得的几何体的体积为( )A.12π B.16π C.20π D.24π【解析】 旋转后的几何体为以 AC=4 为底面半径,以 3 为高的圆锥,V=πr2h=π×42×3=16π.【答案】 B[小组合作型]柱体的体积 如图 1714① 是一个水平放置的正三棱柱 ABCA1B1C1,D 是棱 BC 的中点.正三棱柱的主视图如图 1714②.求正三棱柱 ABCA1B1C1的体积.图 1714【精彩点拨】 先利用主视图中的数据确定出正三棱柱底面边长及侧棱长,再代入柱体的体积公式求解.【自主解答】 由三视图可知:在正三棱柱中,AD=,AA1=3,从而在底面即等边△ABC 中,AB===2,所以正三棱柱的体积V=Sh=×BC×AD×AA1=×2××3=3.计算柱体体积的关键及常用技巧:(1)计算柱体体积的关键:确定柱体的底面积和高.(2)常用技巧:① 充分利用多面体的截面及旋转体的轴截面,构造直角三角形,从而计算出底面积和高.② 由于柱体的体积仅与它的底面积和高有关,而与柱体是几棱柱,是直棱柱还是斜棱柱没有关系,所以我们往往把求斜棱柱的体积通过作垂直于侧棱的截面转化成求直棱柱的体积.[再练一题]1.一个正方体的底面积和一个圆柱的底面积相等,且侧面积也相等,求正方体和圆柱的体积之比. 【导学号:39292050】【解】 设正方体边长为 a,圆柱高为 h,底面半径为 r,则有由①得 r=a,由②得 πrh=2a2,∴V 圆柱=πr2h=a3,∴V 正方体∶V 圆柱=a3∶=∶1=∶2.锥体的体积 一个正三棱锥底面边长为 6,侧棱长为,求这个三棱锥体积.【精彩点拨】 已知底面边长和侧棱长,可先求出三棱锥的底面积和高,再根据体积公式求出其体积.【自主解答】 如图所示,正三棱锥 SABC.设 H 为正三角形 ABC 的中心,连接 SH,则 SH 的长即为该正三棱锥的高.连接 AH 并延长交 BC 于 E,则 E 为 BC 的中点,且 AH⊥BC. △ABC 是边长为 6 的正三角形,∴AE=×6=3,∴AH=...