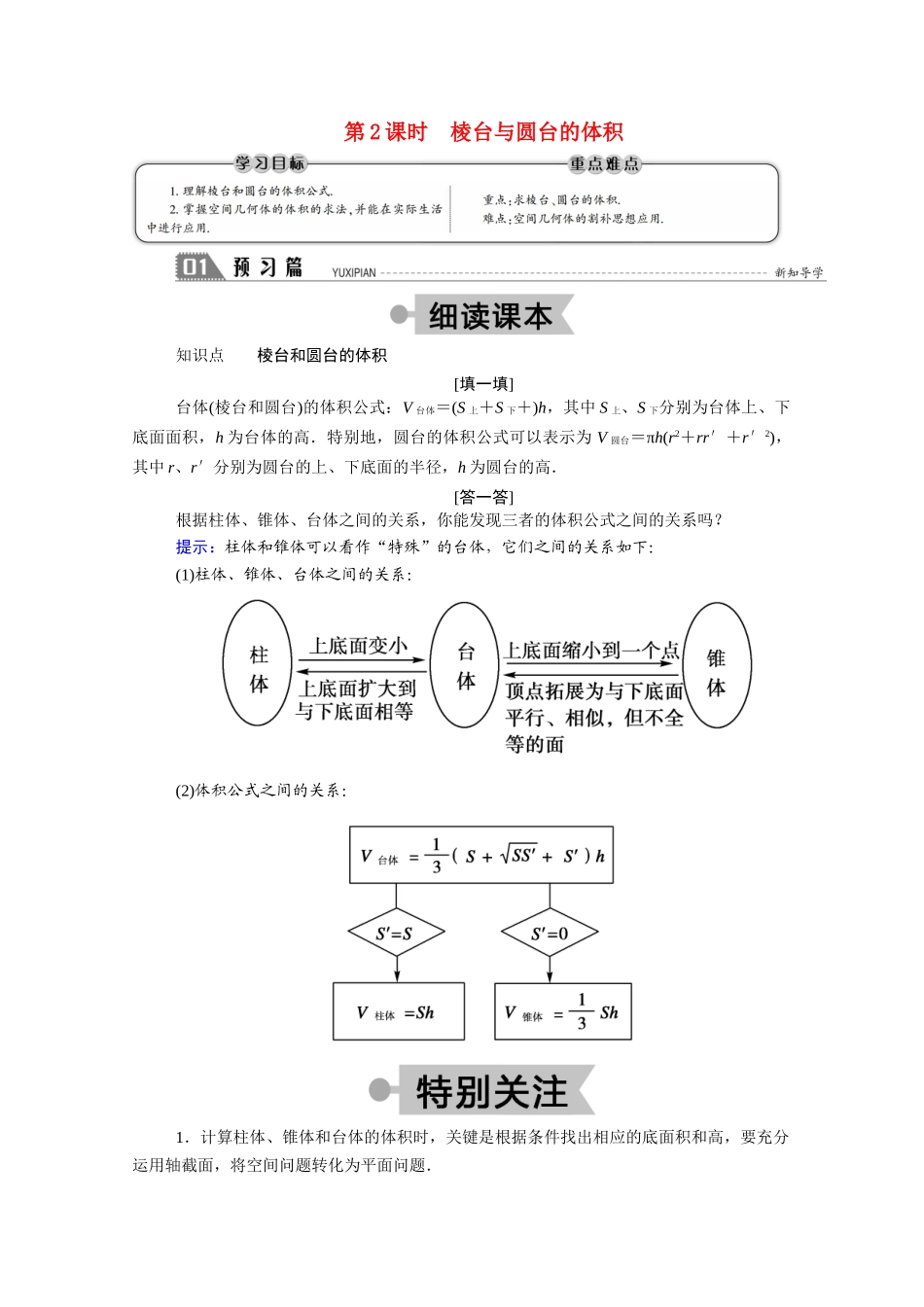
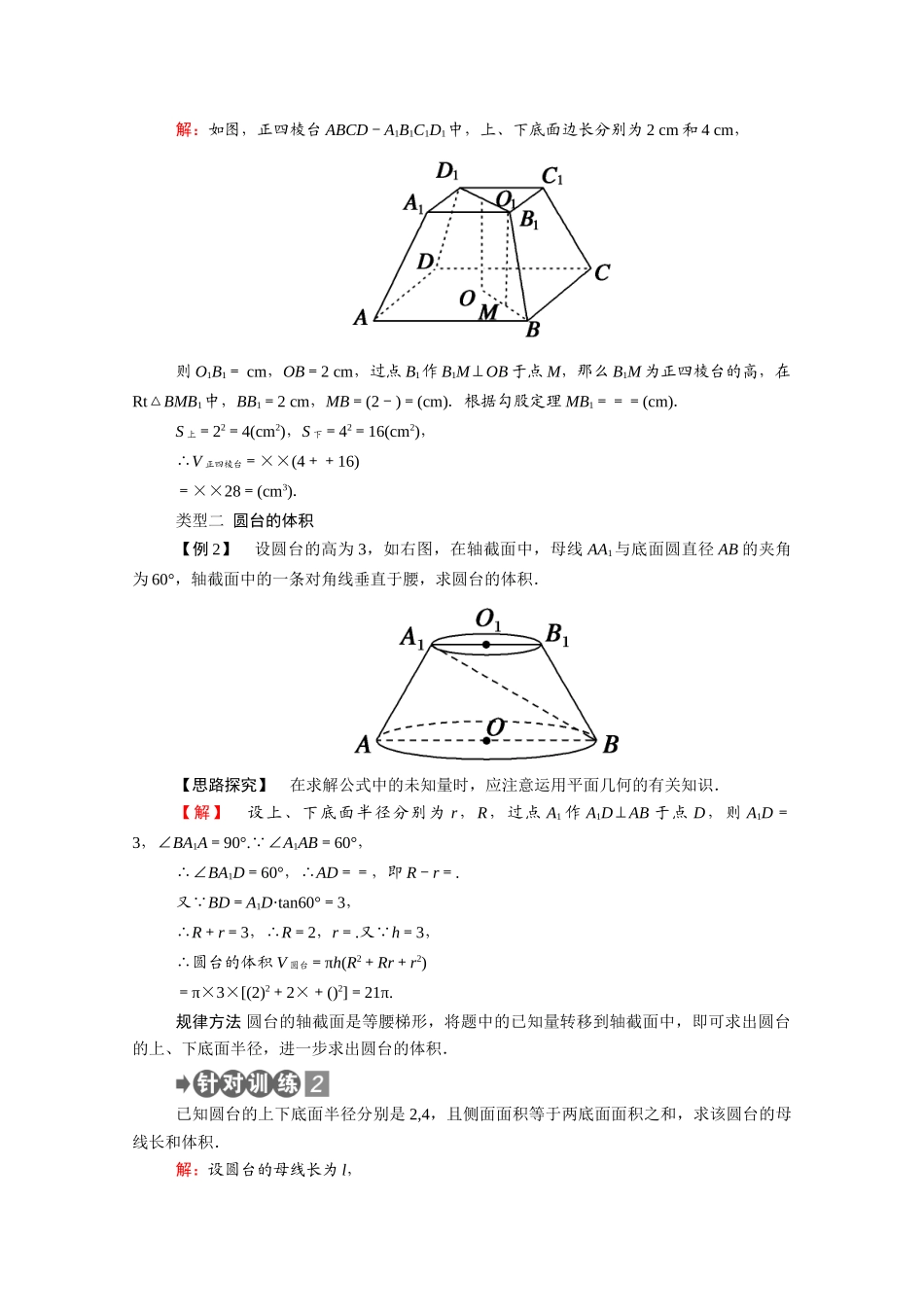
第 2 课时 棱台与圆台的体积知识点 棱台和圆台的体积 [填一填]台体(棱台和圆台)的体积公式:V 台体=(S 上+S 下+)h,其中 S 上、S 下分别为台体上、下底面面积,h 为台体的高.特别地,圆台的体积公式可以表示为 V 圆台=πh(r2+rr′+r′2),其中 r、r′分别为圆台的上、下底面的半径,h 为圆台的高.[答一答]根据柱体、锥体、台体之间的关系,你能发现三者的体积公式之间的关系吗?提示:柱体和锥体可以看作“特殊”的台体,它们之间的关系如下:(1)柱体、锥体、台体之间的关系:(2)体积公式之间的关系:1.计算柱体、锥体和台体的体积时,关键是根据条件找出相应的底面积和高,要充分运用轴截面,将空间问题转化为平面问题.2.对于圆台问题,注意“补台为锥”的思想方法.3.割补法求体积当一个几何体的形状不规则时,无法直接运用体积公式求解,这时一般通过分割与补形,将原几何体分割或补形成较易计算体积的几何体,从而求出原几何体的体积,这种方法就称为割补法.此时应注意分割过程中的等积特点,切不可出现重复和遗漏.类型一 棱台的体积 【例 1】 已知正四棱台两底面边长分别为 20 cm 和 10 cm,侧面积是 780 cm2.求正四棱台的体积.【思路探究】 可以尝试借助四棱台内的直角梯形.求出棱台底面积和高,从而求出体积.【解】 如图所示,正四棱台 ABCD-A1B1C1D1中,A1B1=10 cm,AB=20 cm.取 A1B1的中点 E1,AB 的中点 E,则 E1E 是侧面 ABB1A1的高.设 O1、O 分别是上、下底面的中心,则四边形 EOO1E1是直角梯形.由 S 侧=4×(10+20)·E1E=780,得 EE1=13,在直角梯形 EOO1E1中,O1E1=A1B1=5,OE=AB=10,∴O1O==12,V 正四棱台=×12×(102+202+10×20)=2 800(cm3).故正四棱台的体积为 2 800 cm3.规律方法 求台体的体积关键是求出上、下底面的面积和台体的高.要注意充分运用棱台内的直角梯形或圆台的轴截面寻求相关量之间的关系.本例若改为“正四棱台的上、下两底的底面边长分别为 2 cm 和 4 cm,侧棱长为 2 cm”,求该棱台的体积.解:如图,正四棱台 ABCD-A1B1C1D1中,上、下底面边长分别为 2 cm 和 4 cm,则 O1B1= cm,OB=2 cm,过点 B1作 B1M⊥OB 于点 M,那么 B1M 为正四棱台的高,在Rt△BMB1中,BB1=2 cm,MB=(2-)=(cm).根据勾股定理 MB1===(cm).S 上=22=4(cm2),S 下=42=16(cm2),∴V 正四棱台=××(4+...