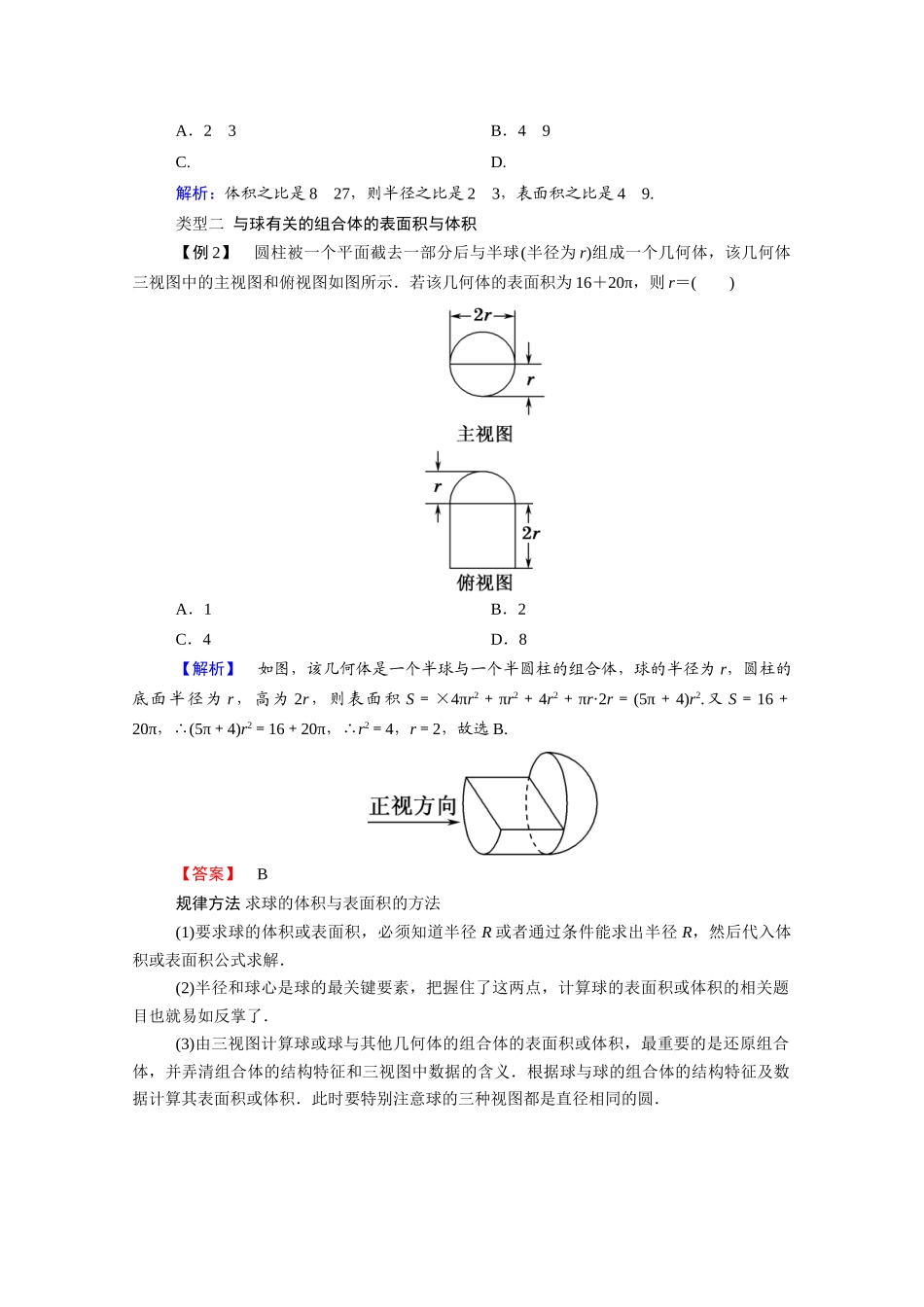
7.3 球知识点 球的表面积与体积 [填一填]1.球的体积球的半径为 R,那么它的体积是 V=πR3.2.球的表面积球的半径为 R,那么它的表面积是 S=4π R 2 .[答一答]怎样分析与球有关的组合体问题?提示:通过画过球心的截面来分析.例如,底面半径为 r,高为 h 的圆锥内部有一球O,且球与圆锥的底面和侧面均相切.过球心 O 作球的截面,如图所示,则球心是等腰三角形 ABC 的内切圆的圆心,AB 和 AC 均是圆锥的母线,BC 是圆锥底面直径,D 是圆锥底面的圆心.用同样的方法可得以下结论:① 长方体的 8 个顶点在同一个球面上,则长方体的体对角线是球的直径;球与正方体的六个面均相切,则球的直径等于正方体的棱长;球与正方体的 12 条棱均相切,则球的直径是正方体的面对角线.② 球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径.③ 球与圆台的底面和侧面均相切,则球的直径等于圆台的高.1.球的体积和表面积都是关于半径 R 的函数,因此求体积和表面积时,只需求出半径即可.2.确定一个球的条件是球心和球的半径,已知球的半径可以利用公式求它的表面积和体积;反过来已知体积或表面积也可以求其半径.3.球的截面在解决球的有关计算问题中起着关键的作用,要注意球的半径与截面圆半径的关系.类型一 球的表面积 【例 1】 已知:圆柱的底面直径与高都等于球的直径.求证:(1)球的表面积等于圆柱的侧面积;(2)球的表面积等于圆柱表面积的.【证明】 (1)如图,设球的半径为 R,则圆柱的底面半径为 R,高为 2R,得 S 球=4πR2,S 圆柱侧=2πR·2R=4πR2.∴S 球=S 圆柱侧 .(2) S 圆柱表=4πR2+2πR2=6πR2,S 球=4πR2,∴S 球=S 圆柱表 .规律方法 要解决两几何体间的体积(面积)关系,必须首先算出球的体积(表面积)与圆柱的体积(侧面积),算出球的体积(表面积)与圆柱的体积(侧面积)要知道球的半径,球的半径可设为 R.(1)球的体积是 π,则此球的表面积是( B )A.12π B.16πC.π D.π解析:πR3=π,故 R=2,球的表面积为 4πR2=16π.(2)两个球的体积之比是 827,那么这两个球的表面积之比是( B )A.23 B.49C. D.解析:体积之比是 827,则半径之比是 23,表面积之比是 49.类型二 与球有关的组合体的表面积与体积 【例 2】 圆柱被一个平面截去一部分后与半球(半径为 r)组成一个几何体,该几何体三视图中的主视...