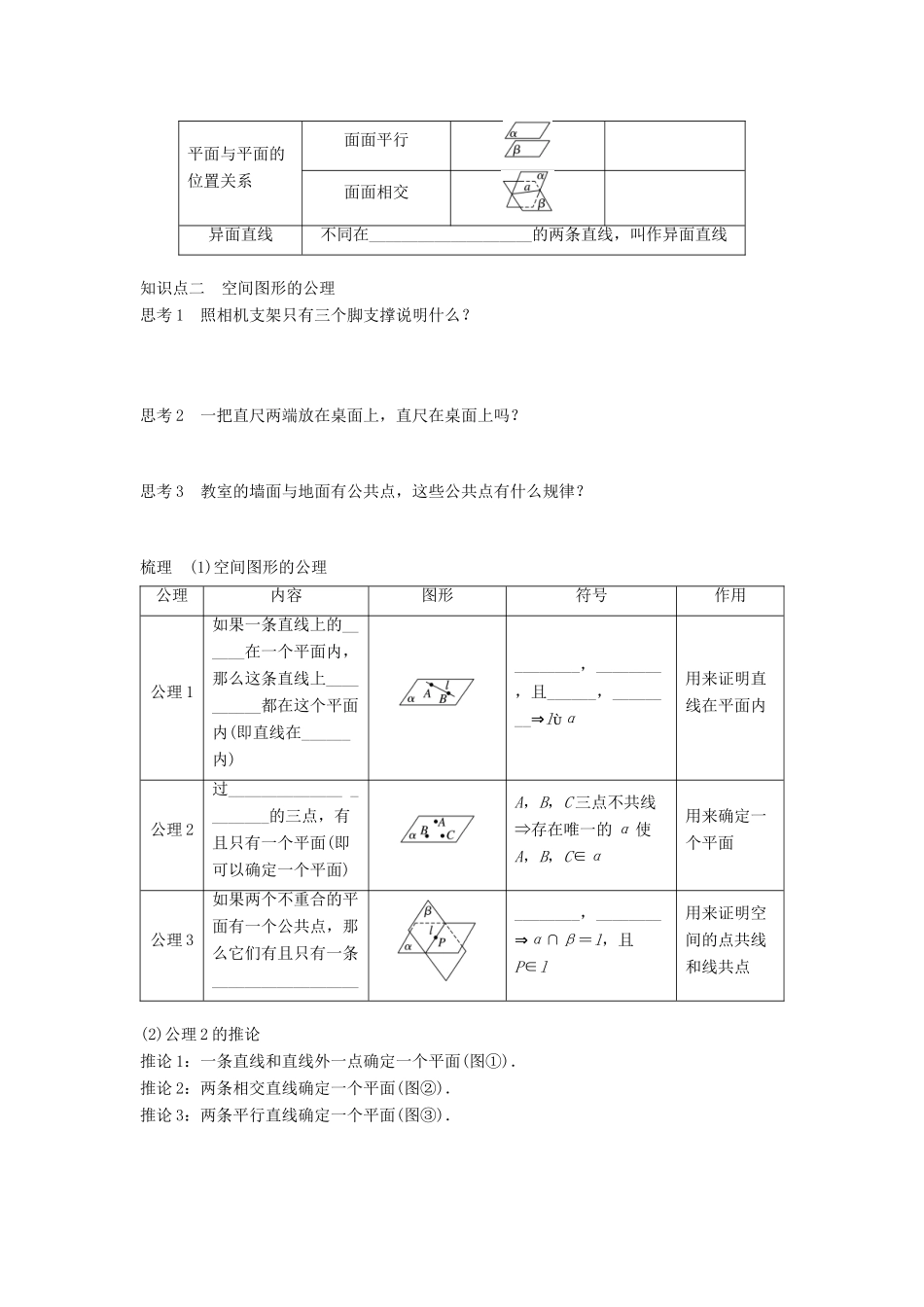
4.1 空间图形基本关系的认识4.2 空间图形的公理(一)学习目标 1.通过长方体这一常见的空间图形,体会点、直线、平面之间的位置关系.2.会用符号表达点、线、面的位置关系.3.掌握空间图形的三个公理及其推论.知识点一 空间图形的基本位置关系对于长方体有 12 条棱和 6 个面.思考 1 12 条棱中,棱与棱有几种位置关系? 思考 2 棱所在直线与面之间有几种位置关系? 思考 3 六个面之间有哪几种位置关系. 梳理 位置关系图形表示符号表示点与直线的位置关系点 A 在直线 a 外A∉a点 B 在直线 a 上B∈a点与平面的位置关系点 A 在平面 α 内A∈α点 B 在平面 α 外B∉α直线与直线的位置关系平行a∥b相交异面a 与 b 异面直线与平面的位置关系线在面内线面相交线面平行平面与平面的位置关系面面平行面面相交异面直线不同在____________________的两条直线,叫作异面直线知识点二 空间图形的公理思考 1 照相机支架只有三个脚支撑说明什么? 思考 2 一把直尺两端放在桌面上,直尺在桌面上吗? 思考 3 教室的墙面与地面有公共点,这些公共点有什么规律? 梳理 (1)空间图形的公理公理内容图形符号作用公理 1如果一条直线上的______在一个平面内,那么这条直线上__________都在这个平面内(即直线在______内)________,________,且______,________⇒lα用来证明直线在平面内公理 2过______________ ________的三点,有且只有一个平面(即可以确定一个平面)A,B,C 三点不共线⇒存在唯一的 α 使A,B,C∈α用来确定一个平面公理 3如果两个不重合的平面有一个公共点,那么它们有且只有一条__________________________,________⇒α∩β=l,且P∈l用来证明空间的点共线和线共点(2)公理 2 的推论推论 1:一条直线和直线外一点确定一个平面(图①).推论 2:两条相交直线确定一个平面(图②).推论 3:两条平行直线确定一个平面(图③).类型一 文字语言、图形语言、符号语言的相互转化例 1 根据图形用符号表示下列点、直线、平面之间的关系.(1)点 P 与直线 AB;(2)点 C 与直线 AB;(3)点 M 与平面 AC;(4)点 A1与平面 AC;(5)直线 AB 与直线 BC;(6)直线 AB 与平面 AC;(7)平面 A1B 与平面 AC. 反思与感悟 (1)用文字语言、符号语言表示一个图形时,首先仔细观察图形有几个平面、几条直线且相互之间的位置关系如何,试着用文字语言表示,再用符号语言表示.(2)根据符号语...