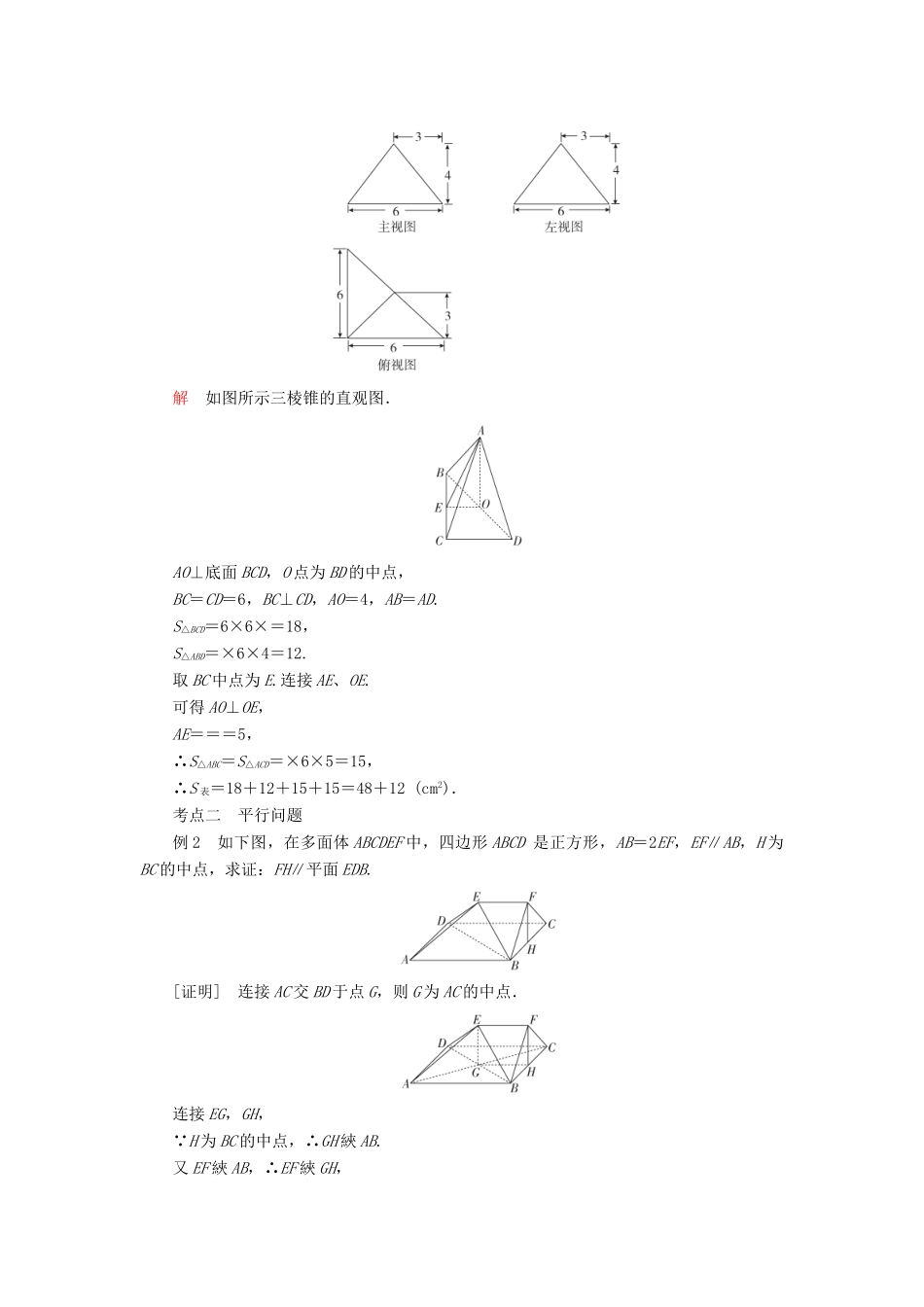
第一章 立体几何初步 知识网络构建 高频考点例析考点一 空间几何体的直观图和三视图例 1 一个几何体的三视图如图所示,则该几何体的体积为________.[解析] 由三视图可知该组合体的上方是一个高为 1,底面直径为 2 的圆柱,下方是一个长宽高分别为 4,3,1 的长方体,它的体积 V=1×π×12+4×3×1=12+π.[答案] 12+π类题通法由三视图求几何体的表面积与体积的综合题,是新课标高考题的一个热点,解这类题往往由三视图想象原貌,考察其结构特征及其组合状况,再根据三视图中所标基本量,利用面积、体积公式计算结果. 一个棱锥的三视图如图,求该棱锥的表面积(单位:cm2).解 如图所示三棱锥的直观图.AO⊥底面 BCD,O 点为 BD 的中点,BC=CD=6,BC⊥CD,AO=4,AB=AD.S△BCD=6×6×=18,S△ABD=×6×4=12.取 BC 中点为 E.连接 AE、OE.可得 AO⊥OE,AE===5,∴S△ABC=S△ACD=×6×5=15,∴S 表=18+12+15+15=48+12 (cm2).考点二 平行问题例 2 如下图,在多面体 ABCDEF 中,四边形 ABCD 是正方形,AB=2EF,EF∥AB,H 为BC 的中点,求证:FH∥平面 EDB.[证明] 连接 AC 交 BD 于点 G,则 G 为 AC 的中点.连接 EG,GH, H 为 BC 的中点,∴GH 綊 AB.又 EF 綊 AB,∴EF 綊 GH,∴四边形 EFHG 为平行四边形,∴EG∥FH, EG平面 EDB,FH⊆平面 EDB,∴FH∥平面 EDB.类题通法在解决线面、面面平行问题时,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行”,而利用性质定理时,其顺序相反,且“高维”的性质定理就是“低维”的判定定理.特别注意,转化的方法总是由具体题目的条件决定,不能过于呆板僵化,遵循规律而不受制于规律. 如图所示,在直四棱柱 ABCD-A1B1C1D1 中,底面是正方形,E,F,G 分别是棱B1B、D1D、DA 的中点.求证:平面 AD1E∥平面 BGF.证明 E,F 分别是 B1B 和 D1D 的中点,∴D1F 綊 BE,∴BED1F 是平行四边形,∴D1E∥BF,又 D1E⊆平面 BGF,BF平面 BGF,∴D1E∥平面 BGF. FG 是△DAD1的中位线,∴FG∥AD1.又 AD1⊆平面 BGF,FG平面 BGF,∴AD1∥平面 BGF.又 AD1∩D1E=D1,∴平面 AD1E∥平面 BGF.考点三 垂直问题例 3 如图,在四棱锥 S-ABCD 中,底面 ABCD 是正方形,SA⊥平面 ABCD,且 SA=AB,点 E 是 AB 的中点,点 F 是 SC 的中点.求...