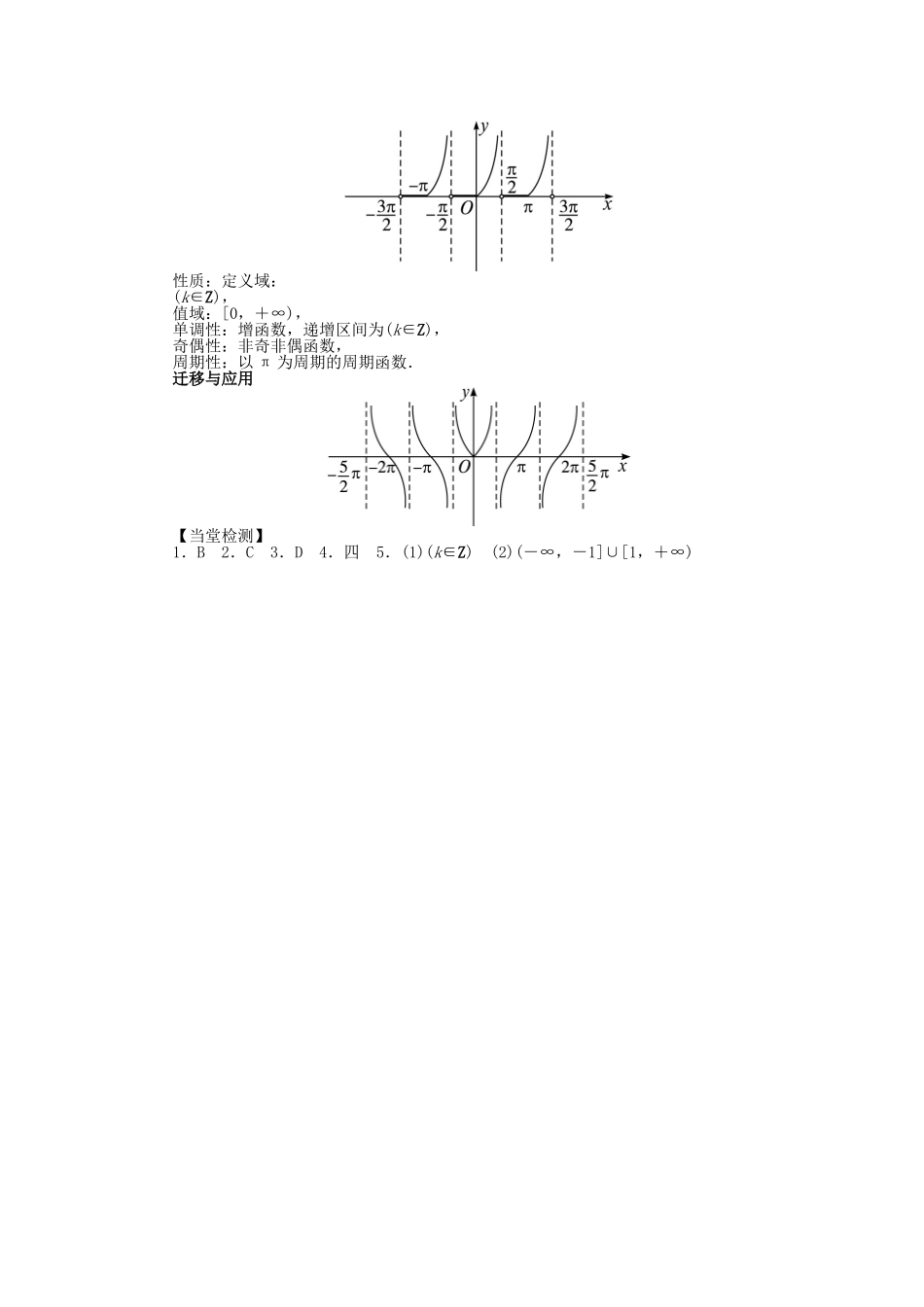
1.7.2 正切函数的图像与性质问题导学1.正切函数的定义及应用活动与探究 1若 tan α=,借助三角函数的定义求角 α 的正弦函数值和余弦函数值.迁移与应用已知角 α 的终边经过点 P(1,-2),求的值.(1)已知角 α 终边上一点 P(x,y),点 P 到原点 O 的距离 r=|OP|=,则 sin α=,cos α=,tan α=.(2)已知角 α 的正切值,在求它的正弦值和余弦值时,要注意对 α 角所在的象限分类讨论.2.正切函数的定义域、值域问题活动与探究 2(1)求函数 y=的定义域.(2)求函数 y=tan2x-2tan x-3 在区间上的值域.迁移与应用求函数 y=tan 的定义域、值域.求与正切函数有关的函数的定义域、值域的方法及应注意的问题.(1)求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数 y=tan x 有意义,即 x≠kπ+(k∈Z).而对于构建的三角不等式,常利用三角函数的图像求解.(2)求解与正切函数有关的函数值域时,要注意函数的定义域,在定义域内求值域;对于求由正切函数复合而成的函数的值域时,常利用换元法,但要注意新“元”的范围.3.正切函数的周期性、单调性活动与探究 3求函数 y=tan 的定义域、最小正周期、单调区间及对称中心.迁移与应用求函数 y=3tan 的周期和单调区间.对正切函数的周期性与单调性的解读:(1)函数 y=Atan(ωx+φ)(ω>0)的最小正周期为 T=.(2)正切函数在每一个单调区间内是增函数,但在整个定义域上不是增函数.(3)求函数 y=Atan(ωx+φ)(ω>0)的定义域、单调区间、对称中心等时,常采用“整体代换”的思想,把 ωx+φ 作为一个整体,依据函数 y=tan x 的定义域,单调区间及对称中心来求解.4.利用函数图像研究函数性质活动与探究 4利用正切函数的图像作出 y=tan x+|tan x|的图像,并根据图像研究其性质.迁移与应用作出函数 y=tan|x|的图像.(1)作函数 y=|f(x)|的图像一般利用图像变换方法,具体步骤是:① 保留函数 y=f(x)的图像在 x 轴上方的部分;② 将函数 y=f(x)的图像在 x 轴下方的部分沿 x 轴向上翻折.(2)若函数为周期函数,可先研究其一个周期上的图像,再利用周期性,延拓到定义域上即可.当堂检测1.函数 y=tan 2x 的最小正周期是( ).A. B. C.π D.2π2.在下列函数中,同时满足:①在上递增;②以 2π 为周期;③是奇函数的是( ).A.y=|tan x| B.y=cos xC.y=ta...