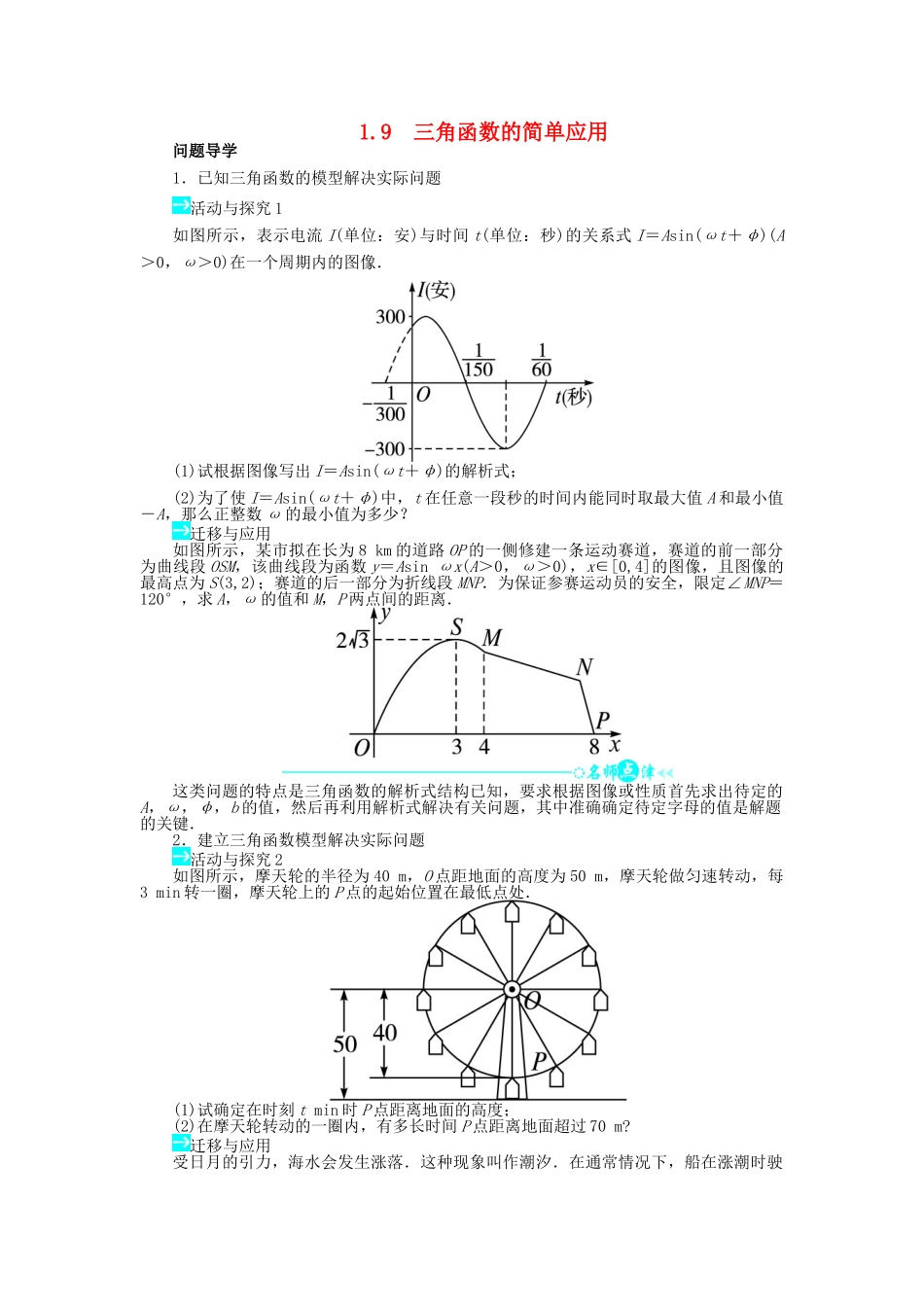
1.9 三角函数的简单应用问题导学1.已知三角函数的模型解决实际问题活动与探究 1如图所示,表示电流 I(单位:安)与时间 t(单位:秒)的关系式 I=Asin(ωt+φ)(A>0,ω>0)在一个周期内的图像.(1)试根据图像写出 I=Asin(ωt+φ)的解析式;(2)为了使 I=Asin(ωt+φ)中,t 在任意一段秒的时间内能同时取最大值 A 和最小值-A,那么正整数 ω 的最小值为多少?迁移与应用如图所示,某市拟在长为 8 km 的道路 OP 的一侧修建一条运动赛道,赛道的前一部分为曲线段 OSM,该曲线段为函数 y=Asin ωx(A>0,ω>0),x∈[0,4]的图像,且图像的最高点为 S(3,2);赛道的后一部分为折线段 MNP.为保证参赛运动员的安全,限定∠MNP=120°,求 A,ω 的值和 M,P 两点间的距离.这类问题的特点是三角函数的解析式结构已知,要求根据图像或性质首先求出待定的A,ω,φ,b 的值,然后再利用解析式解决有关问题,其中准确确定待定字母的值是解题的关键.2.建立三角函数模型解决实际问题活动与探究 2如图所示,摩天轮的半径为 40 m,O 点距地面的高度为 50 m,摩天轮做匀速转动,每3 min 转一圈,摩天轮上的 P 点的起始位置在最低点处.(1)试确定在时刻 t min 时 P 点距离地面的高度;(2)在摩天轮转动的一圈内,有多长时间 P 点距离地面超过 70 m?迁移与应用受日月的引力,海水会发生涨落.这种现象叫作潮汐.在通常情况下,船在涨潮时驶进航道靠近船坞;卸货后落潮时返回海洋.某港口水的深度 y(米)是时间 t(0≤t≤24,单位:时)的函数,记作 y=f(t),下面是某日水深的数据:t(时)03691215182124y(米)10.013.09.97.010.013.010.17.010.0经长期观察,y=f(t)的曲线可以近似地看成函数 y=Asin ωt+b 的图像.(1)试根据以上数据,求出函数 y=f(t)的近似表达式;(2)一般情况下,船舶航行时,船底离海底的距离为 5 米或 5 米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).某船吃水深度(船底离水面的距离)为 6.5 米,如果该船希望在同一天内安全进出港,请问:它至多能在港内停留多长时间(忽略进出港所需的时间)?解决这类问题首先要建立坐标系,根据题意确定函数的解析式,然后再解决相关问题.3.三角函数的最值问题活动与探究 3如图所示,ABCD 是一块边长为 100 m 的正方形地皮,其中 AST 是一半径为 90 m 的扇形小山,其余部分都是平地,一开发商想在平地上建一个矩形停...