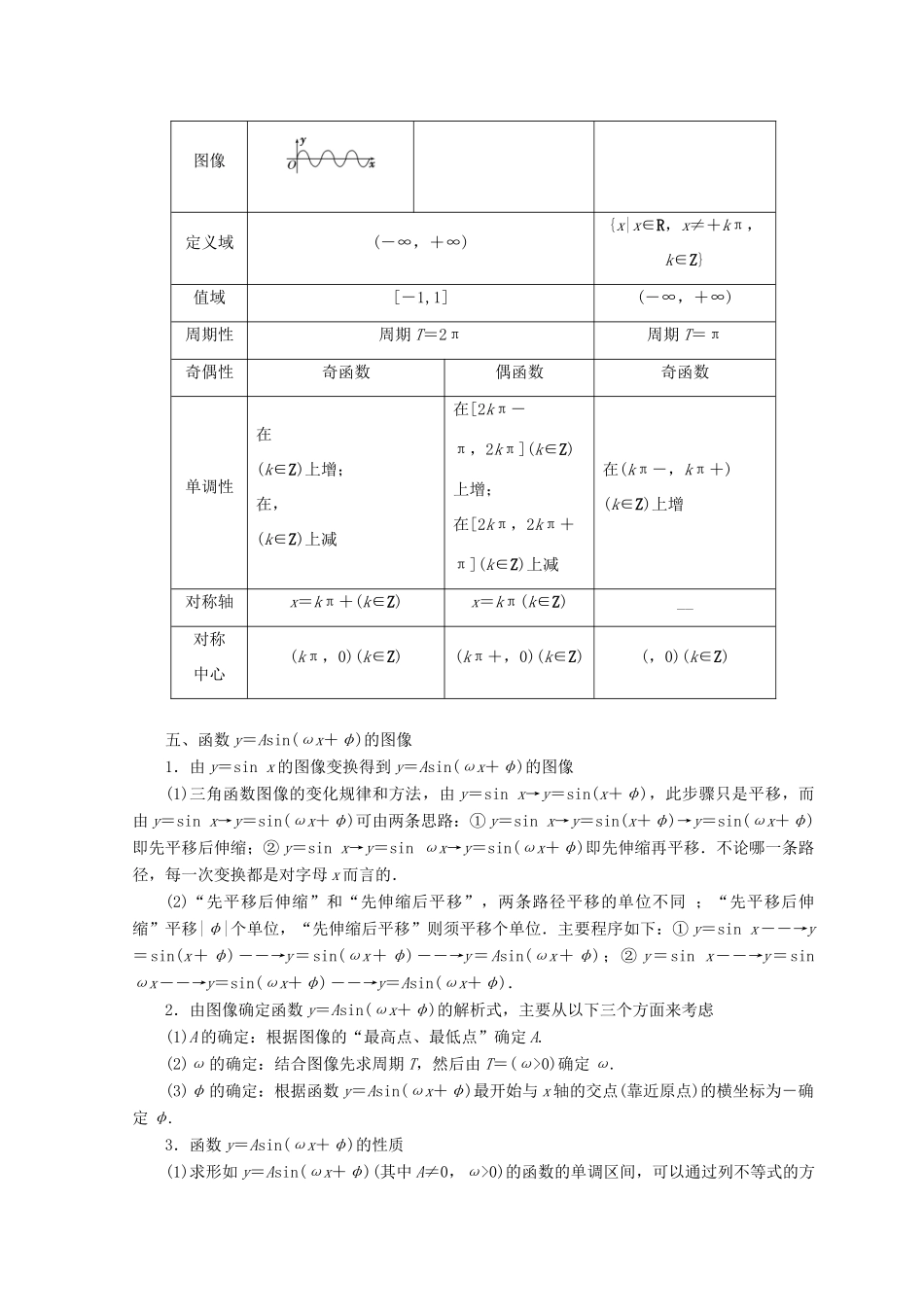
第一章 三角函数一、角的概念1.角不仅有大小而且有正负,角的概念的推广重在“旋转”两字.其旋转方向决定了角的正负,由此确定了角的分类.2.象限角及非象限角,都是相对于坐标系而言的,应注意平面直角坐标系的建立方法,即角的顶点与坐标原点重合,角的始边与 x 轴的正半轴重合,只有在这一前提下,才能讨论象限角与非象限角.3.终边相同的角有无数个,在所有与角 α 终边相同的角的集合可表示为 S=.终边相同的角不一定相等,但相等的角终边一定相同.二、角度制与弧度制弧度制是以“弧度”为单位来度量角的单位制,而角度制是以“度”为单位来度量角的单位制,两种单位不能混用,如+k×360°或 60°+2kπ,k∈Z 的写法是不允许的,尤其是当角是用字母表示时更要注意,如角是在弧度制下,就不能写成 k×360°+α,k∈Z 等.三、三角函数的定义1.三角函数的定义有两种(1)角 α 的终边上任取一点 P(x,y),|OP|=r,则 sin α=,cos α=;tan α=.(2)角 α 的终边与以原点为圆心,以单位长为半径的圆交于点 P(x,y),则 sin α=y,cos α=x,tan α=.2.用三角函数线解基本的三角不等式的步骤为:(1)先作出取等号的角;(2)利用三角函数线的直观性,在单位圆中确定满足不等式的角范围.3.诱导公式2kπ+α,π±α,-α,2π±α,±α 的诱导公式可归纳为:k×+α(k∈Z)的三角函数值.当 k 为偶数时,得 α 的同名三角函数值;当 k 为奇数时,得 α 的余名三角函数值,然后在前面加上一个把 α 看成锐角时原函数值的符号,概括为“奇变偶不变,符号看象限”,这里的奇偶指整数 k 的奇偶.四、三角函数的图像与性质y=sin xy=cos xy=tan x图像定义域(-∞,+∞){x|x∈R,x≠+kπ,k∈Z}值域[-1,1](-∞,+∞)周期性周期 T=2π周期 T=π奇偶性奇函数偶函数奇函数单调性在(k∈Z)上增;在,(k∈Z)上减在[2kπ-π,2kπ](k∈Z)上增;在[2kπ,2kπ+π](k∈Z)上减在(kπ-,kπ+)(k∈Z)上增对称轴x=kπ+(k∈Z)x=kπ(k∈Z)__对称中心(kπ,0)(k∈Z)(kπ+,0)(k∈Z)(,0)(k∈Z)五、函数 y=Asin(ωx+φ)的图像1.由 y=sin x 的图像变换得到 y=Asin(ωx+φ)的图像(1)三角函数图像的变化规律和方法,由 y=sin x→y=sin(x+φ),此步骤只是平移,而由 y=sin x→y=sin(ωx+φ)可由两条思路:① y=sin x→y=sin(x+φ)→y=sin(ωx+φ)即先平移后伸缩;② ...