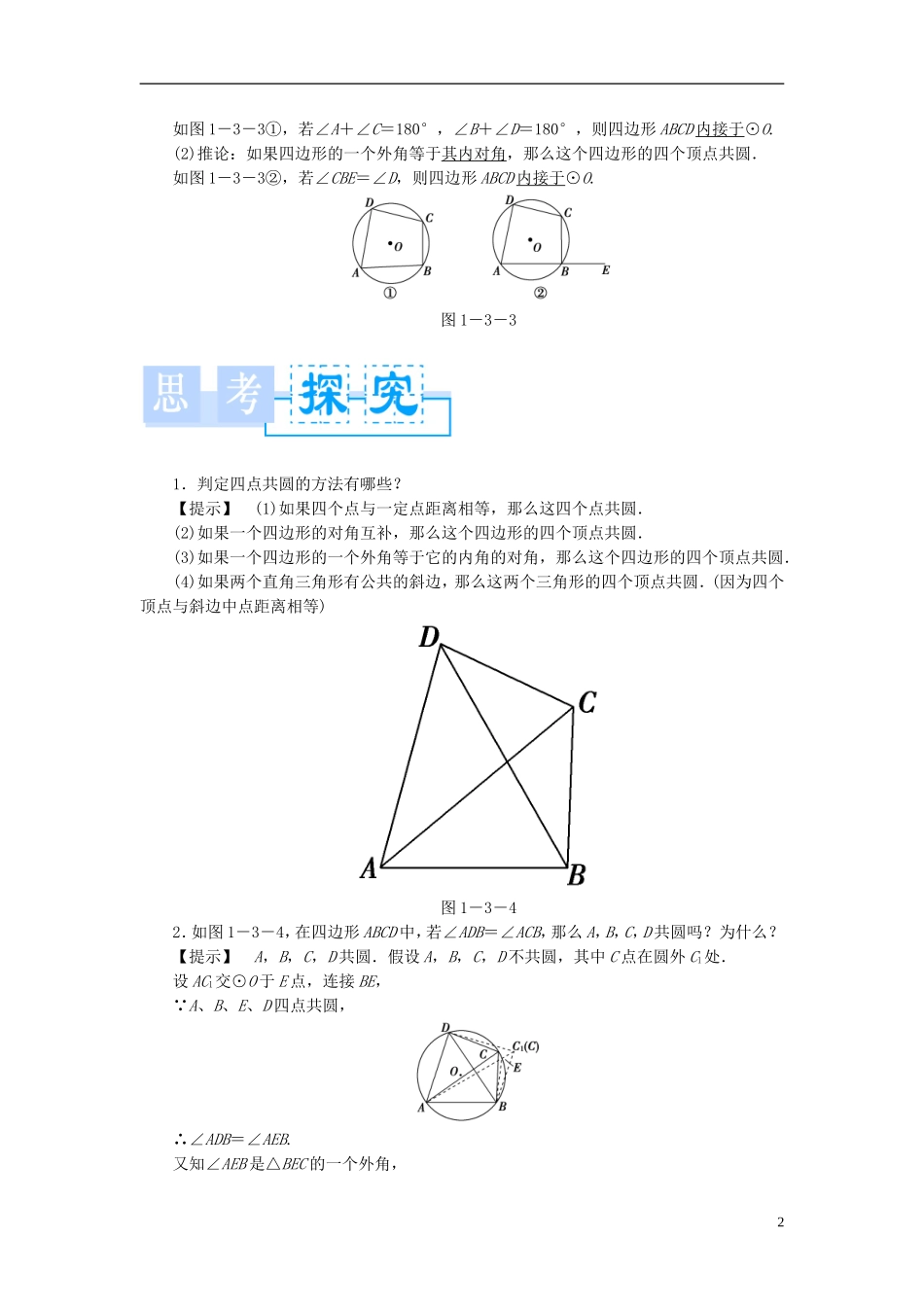
1.3.1 圆内接四边形课标解读1.了解圆内接四边形的概念.2.掌握并灵活运用圆内接四边形的性质定理与判定定理及其推论.图 1-3-11.圆内接四边形的性质定理及推论(1)圆内接四边形的性质定理圆内接四边形的对角互补.如图 1-3-1,四边形 ABCD 内接于⊙O,则有:∠A+∠ C =180°,∠B+∠ D =180°.(2)推论图 1-3-2圆内接四边形的任何一个外角都等于它的内对角.如图 1-3-2,∠CBE 是圆内接四边形 ABCD 的一外角,则有:∠CBE=∠ D .2.圆内接四边形的判定定理及推论(1)判定定理:如果一个四边形的内对角互补,那么这个四边形四个顶点共圆.1如图 1-3-3①,若∠A+∠C=180°,∠B+∠D=180°,则四边形 ABCD 内接于⊙O.(2)推论:如果四边形的一个外角等于其内对角,那么这个四边形的四个顶点共圆.如图 1-3-3②,若∠CBE=∠D,则四边形 ABCD 内接于⊙O.图 1-3-31.判定四点共圆的方法有哪些?【提示】 (1)如果四个点与一定点距离相等,那么这四个点共圆.(2)如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.(3)如果一个四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.(4)如果两个直角三角形有公共的斜边,那么这两个三角形的四个顶点共圆.(因为四个顶点与斜边中点距离相等)图 1-3-42.如图 1-3-4,在四边形 ABCD 中,若∠ADB=∠ACB,那么 A,B,C,D 共圆吗?为什么?【提示】 A,B,C,D 共圆.假设 A,B,C,D 不共圆,其中 C 点在圆外 C1处.设 AC1交⊙O 于 E 点,连接 BE, A、B、E、D 四点共圆,∴∠ADB=∠AEB.又知∠AEB 是△BEC 的一个外角,2∴∠AEB>∠ACB,∴∠ADB>∠ACB,这与∠ADB=∠ACB 矛盾.∴假设不成立.同理若 C1(C)点在⊙O 内,则有:∠ACB>∠ADB,与∠ADB=∠ACB 矛盾.因此A、B、C、D共圆.圆内接四边形的性质图 1-3-5 如图 1-3-5,在 Rt△ABC 中,∠ACB=90°,在 AB 上截取 PA=AC,以PC 为直径的圆分别交 AB、BC、AC 于 D、E、F.求证:=.【思路探究】 先利用 PC 是圆的直径,得到 PF∥BC,再利用圆内接四边形的性质,得到DF∥PC,最后利用平行线分线段成比例证明结论.【自主解答】 连接 DF、PF. PC 是直径,∴PF⊥AC. BC⊥AC,∴PF∥BC,∴=. 四边形 PCFD 内接于⊙O,∴∠ADF=∠ACP, AP=AC,∴∠APC=∠ACP.∴∠ADF=∠APC.∴DF∥PC,3∴=,∴=.1.在本题的证明过程中...