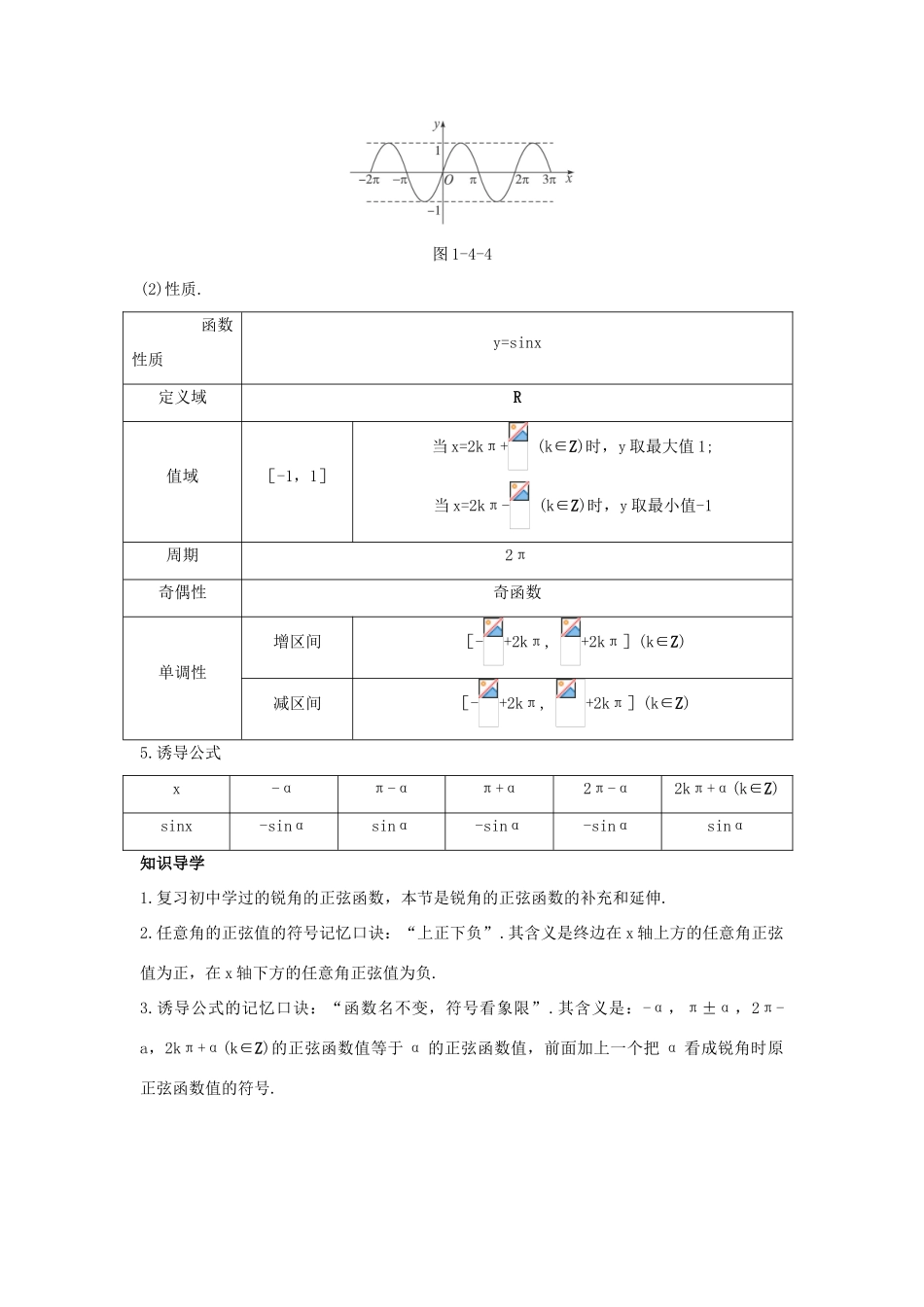
1.5 正弦函数的图像与性质知识梳理1.任意角的正弦函数(1)单位圆:圆心在原点 O,半径等于 1 的圆称为单位圆.(2)定义如图 1-4-1 所示,单位圆与角 α 的终边交于 P 点.设 P(a,b),则 P 点纵坐标 b 是角 α 的函数,称为正弦函数,记为 b=sinα(α∈R).通常用 x、y 表示自变量和因变量,将正弦函数表示为 y=sinx(x∈R).图 1-4-1(3)正弦线如图 1-4-1 所示,过点 P 作 x 轴的垂线 PM,垂足为 M.单位圆中的有向线段 MP 叫做角 α 的正弦线.当角 α 的终边在 x 轴上时,M 与 P 重合,此时正弦线变成一个点.(4)正弦线所表示的正弦值可如下确定:正弦线的方向是表示正弦值的符号,同 y 轴一致,向上为正,向下为负;正弦线的长度是正弦值的绝对值.(5)正弦函数定义的推广如图 1-4-2 所示,设 P(x,y)是 α 的终边上任意一点,图 1-4-2P 到原点的距离|OP|=r,有 r=,则 sinα=.对于每一个确定的角 α,总有唯一确定的正弦值与之对应,所以这个对应法则是以角 α为自变量的函数,叫做正弦函数.正弦函数值与点 P 在角 α 终边上的位置无关,只依赖于角 α 的大小.2.周期函数一般地,对于函数 y=f(x),如果存在一个不为零的常数 T,使得当 x 取定义域内的每一个值时,f(x+T)=f(x)都成立,那么就把函数 y=f(x)叫做周期函数,不为零的常数 T 叫做这个函数的周期.对于周期函数来说,如果所有的周期中存在着一个最小的正数,就称它为最小正周期,今后提到的三角函数的周期,如没特别指明,一般都是指它的最小正周期.3.任意角的正弦值的符号(1)图形表示:各象限正弦函数符号,如图 1-4-3 所示.图 1-4-3(2)表格表示.α 的终边sinαx 非负半轴0第一象限+y 非负半轴+第二象限+x 非正半轴0第三象限-y 非正半轴-第四象限-4.正弦函数的图像和性质(1)图像:如图 1-4-4 所示.图 1-4-4(2)性质.函数性质y=sinx定义域R值域[-1,1]当 x=2kπ+ (k∈Z)时,y 取最大值 1;当 x=2kπ- (k∈Z)时,y 取最小值-1周期2π奇偶性奇函数单调性增区间[-+2kπ, +2kπ](k∈Z)减区间[-+2kπ, +2kπ](k∈Z)5.诱导公式x-απ-απ+α2π-α2kπ+α(k∈Z)sinx-sinαsinα-sinα-sinαsinα知识导学1.复习初中学过的锐角的正弦函数,本节是锐角的正弦函数的补充和延伸.2.任意角的正弦值的符号记忆口诀:“上正下负”.其含义是终边在 x 轴上方的任意角正弦值为正,在 x 轴下方的任意角正弦值为负.3.诱导公式的记忆口诀:“函数名不变,符号看象限”.其含义是:-α,π±α,2π-a,2kπ+α(k∈Z)的正弦函数值等于 α 的正弦函数值,前面加上一个把 α 看成锐角时原正弦函数值的符号.