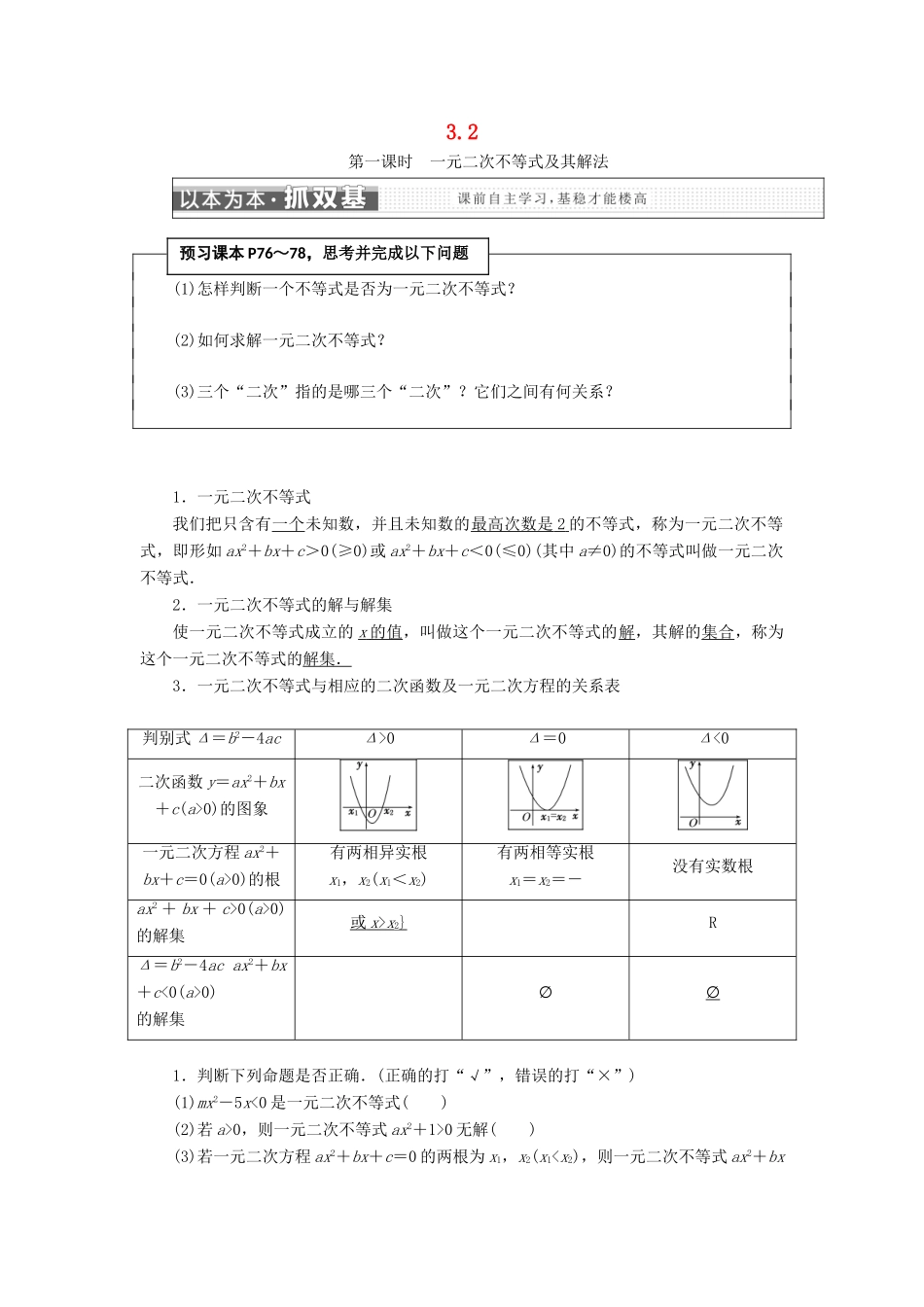
3.2 第一课时 一元二次不等式及其解法(1)怎样判断一个不等式是否为一元二次不等式?(2)如何求解一元二次不等式? (3)三个“二次”指的是哪三个“二次”?它们之间有何关系? 1.一元二次不等式我们把只含有一个未知数,并且未知数的最高次数是 2 的不等式,称为一元二次不等式,即形如 ax2+bx+c>0(≥0)或 ax2+bx+c<0(≤0)(其中 a≠0)的不等式叫做一元二次不等式.2.一元二次不等式的解与解集使一元二次不等式成立的 x 的值 ,叫做这个一元二次不等式的解,其解的集合,称为这个一元二次不等式的解集.3.一元二次不等式与相应的二次函数及一元二次方程的关系表判别式 Δ=b2-4acΔ>0Δ=0Δ<0二次函数 y=ax2+bx+c(a>0)的图象一元二次方程 ax2+bx+c=0(a>0)的根有两相异实根x1,x2(x1<x2)有两相等实根x1=x2=-没有实数根ax2 + bx + c>0(a>0) 的解集或 x > x 2}RΔ=b2-4ac ax2+bx+c<0(a>0) 的解集∅∅1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)(1)mx2-5x<0 是一元二次不等式( )(2)若 a>0,则一元二次不等式 ax2+1>0 无解( )(3)若一元二次方程 ax2+bx+c=0 的两根为 x1,x2(x10 的解集为 R( )解析:(1)错误.当 m=0 时,是一元一次不等式;当 m≠0 时,它是一元二次不等式.(2)错误.因为 a>0,所以不等式 ax2+1>0 恒成立,即原不等式的解集为 R.(3)错误.当 a>0 时,ax2+bx+c<0 的解集为{x|x10 的解集为 R.答案:(1)× (2)× (3)× (4)√2.不等式 x(2-x)>0 的解集为( )A.{x|x>0} B.{x|x<2}C.{x|x>2 或 x<0} D.{x|0<x<2}解析:选 D 原不等式化为 x(x-2)<0,故 0<x<2.3.不等式 x2-2x-5>2x 的解集是( )A.{x|x≥5 或 x≤-1} B.{x|x>5 或 x<-1}C.{x|-12x,得 x2-4x-5>0,因为 x2-4x-5=0 的两根为-1,5,故 x2-4x-5>0 的解集为{x|x<-1 或 x>5}.4.不等式-3x2+5x-4>0 的解集为________.解析:原不等式变形为 3x2-5x+4<0.因为 Δ=(-5)2-4×3×4=-23<0,所以由函数 y=3x2-5x+4 的图象可知,3x2-5x+4<0...