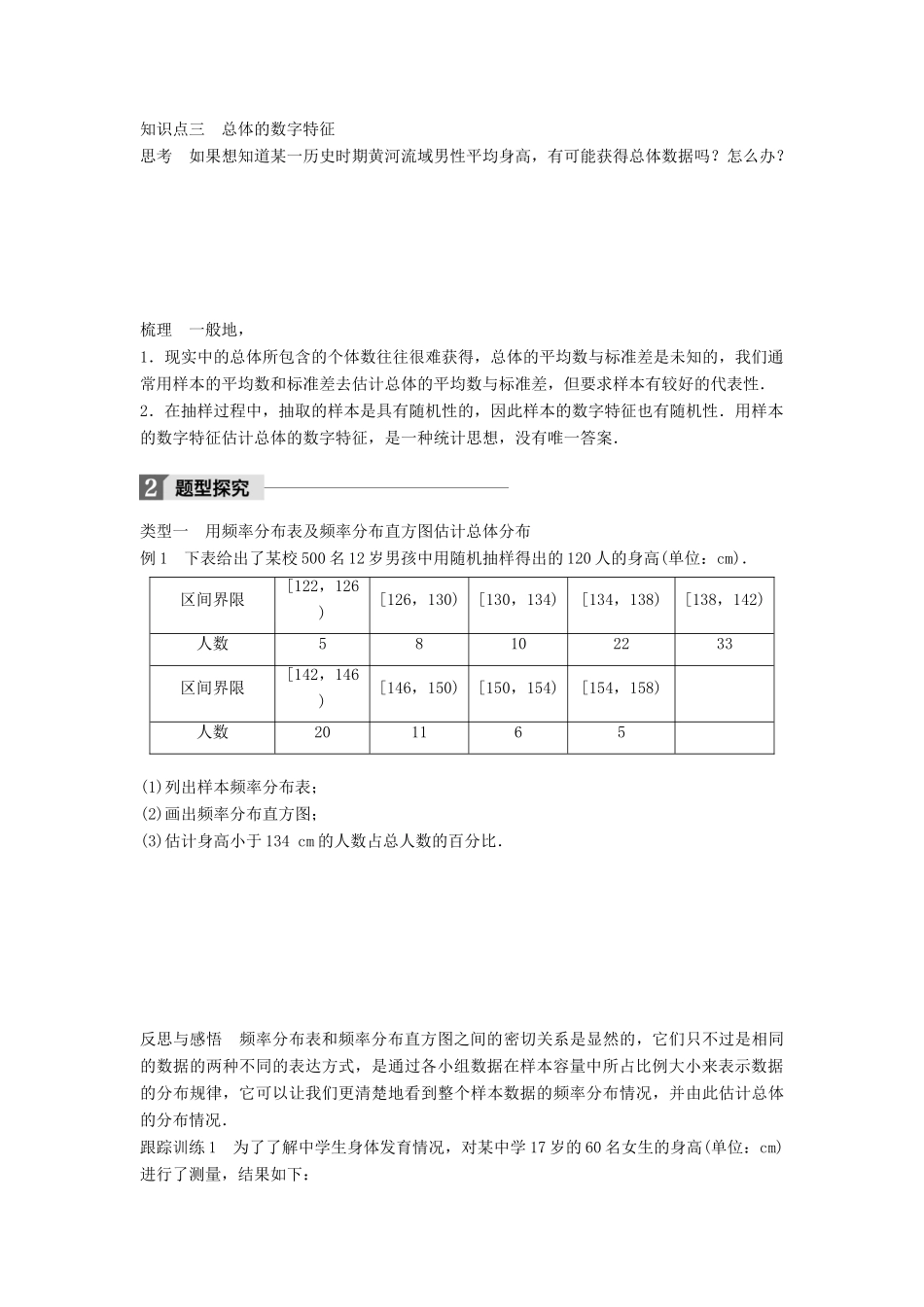
5 用样本估计总体学习目标 1.学会列频率分布表,会画频率分布直方图.2.会用频率分布表或分布直方图估计总体分布,并作出合理解释.3.在解决问题过程中,进一步体会用样本估计总体的思想,认识统计的实际作用,初步经历收集数据到统计数据的全过程.知识点一 总体的分布思考 如果把我国初生婴儿的性别作为总体,那么它的分布是指什么?梳理 一般地,总体分布是指总体中个体所占的比例.知识点二 用频率分布表或频率分布直方图估计总体分布思考 1 要做频率分布表,需要对原始数据做哪些工作? 思考 2 如何决定组数与组距? 思考 3 同样一组数据,如果组距不同,得到的频率分布直方图也会不同吗? 梳理 1.频率分布直方图在频率分布直方图中,纵轴表示,数据落在各小组内的频率用频率分布直方图的________来表示,各小长方形的面积的总和等于____.2.频率折线图在频率分布直方图中,按照分组原则,再在左边和右边各加一个区间,从所加的左边区间的________开始,用线段依次连接各个矩形的____________,直至右边所加区间的________,就可以得到一条折线,我们称之为频率折线图.3.随着样本容量不断增大,样本中落在每个区间内的样本数的________会越来越稳定于总体在相应区间内取值的________.随着样本量的增大,所划分的区间数也可以随之增多,而每个区间的长度则会相应随之减小.相应的频率折线图就会越来越接近于一条光滑曲线.知识点三 总体的数字特征思考 如果想知道某一历史时期黄河流域男性平均身高,有可能获得总体数据吗?怎么办? 梳理 一般地,1.现实中的总体所包含的个体数往往很难获得,总体的平均数与标准差是未知的,我们通常用样本的平均数和标准差去估计总体的平均数与标准差,但要求样本有较好的代表性.2.在抽样过程中,抽取的样本是具有随机性的,因此样本的数字特征也有随机性.用样本的数字特征估计总体的数字特征,是一种统计思想,没有唯一答案.类型一 用频率分布表及频率分布直方图估计总体分布例 1 下表给出了某校 500 名 12 岁男孩中用随机抽样得出的 120 人的身高(单位:cm).区间界限[122,126)[126,130)[130,134)[134,138)[138,142)人数58102233区间界限[142,146)[146,150)[150,154)[154,158)人数201165(1)列出样本频率分布表;(2)画出频率分布直方图;(3)估计身高小于 134 cm 的人数占总人数的百分比. 反思与感悟 频率分布表和频率分布直方图之间的密切关系是显然的...