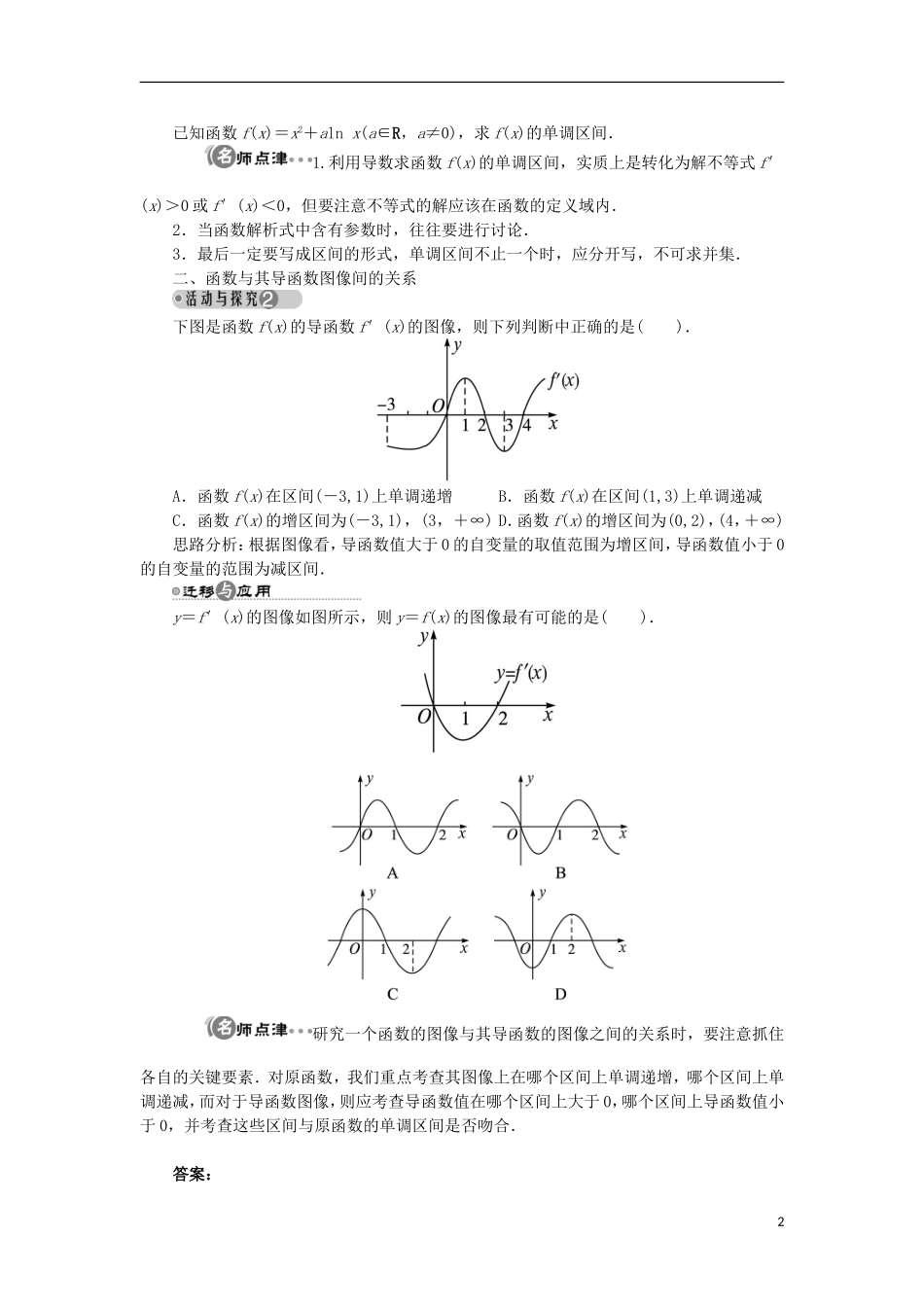
1.1 导数与函数的单调性学习目标重点难点1.结合实例,借助几何直观探索函数的单调性与导数的关系,并能获取一般结论.2.能利用导数研究函数的单调性,会根据导数值的变化规律说出函数值变化快慢的规律.3.会求不超过三次的多项式函数的单调区间.重点:运用导数研究函数的单调性,求不超过三次的多项式函数的单调区间.难点:利用导数求函数的单调区间的步骤,利用导数研究函数的单调性.导数与函数的单调性如果在某个区间内,函数 y=f(x)的导数________,则在这个区间上,函数 y=f(x)是______的.如果在某个区间内,函数 y=f(x)的导数________,则在这个区间上,函数 y=f(x)是______的.预习交流议一议:在某一区间内 f′(x)>0(或 f′(x)<0)是函数 f(x)在该区间上为增(或减)函数的充要条件吗?答案:预习导引f′(x)>0 增加 f′(x)<0 减少预习交流:提示:不是,是充分条件.若在某区间上有限个点使 f′(x)=0,在其余点恒有 f′(x)>0,则 f(x)仍为增函数,如 y=x3,那就是说在某区间上 f′(x)>0 是 f(x)在此区间上为增函数的充分而不必要条件,同理,在某区间上 f′(x)<0 是 f(x)在此区间上为减函数的充分而不必要条件.在预习中还有哪些问题需要你在听课时加以关注?请在下列表格中做个备忘吧!我的学困点我的学疑点一、利用导数求函数的单调区间求下列函数的单调区间:(1)f(x)=x3-4x2+x-1;(2)f(x)=2x-ln x.思路分析:先求导函数 f′(x),再令 f′(x)>0 或 f′(x)<0,求其单调区间.1已知函数 f(x)=x2+aln x(a∈R,a≠0),求 f(x)的单调区间. 1.利用导数求函数 f(x)的单调区间,实质上是转化为解不等式 f′(x)>0 或 f′(x)<0,但要注意不等式的解应该在函数的定义域内.2.当函数解析式中含有参数时,往往要进行讨论.3.最后一定要写成区间的形式,单调区间不止一个时,应分开写,不可求并集.二、函数与其导函数图像间的关系下图是函数 f(x)的导函数 f′(x)的图像,则下列判断中正确的是( ).A.函数 f(x)在区间(-3,1)上单调递增B.函数 f(x)在区间(1,3)上单调递减C.函数 f(x)的增区间为(-3,1),(3,+∞) D.函数 f(x)的增区间为(0,2),(4,+∞)思路分析:根据图像看,导函数值大于 0 的自变量的取值范围为增区间,导函数值小于 0的自变量的范围为减区间.y=f′(x)的图像如图所示,则 y=f(x)的图像最有可能的是( ). 研究一个函数的图像与其导函数的图像之...