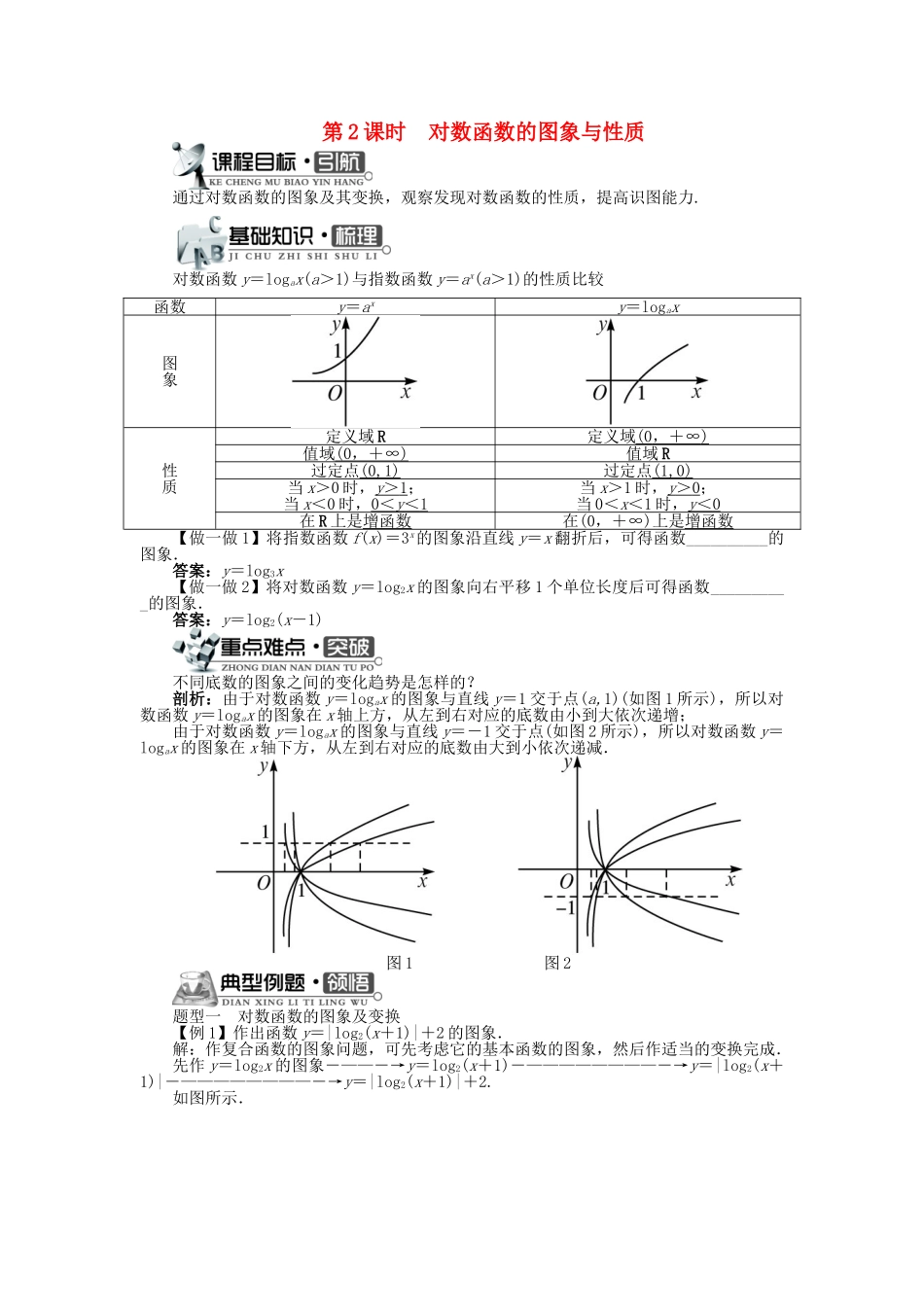
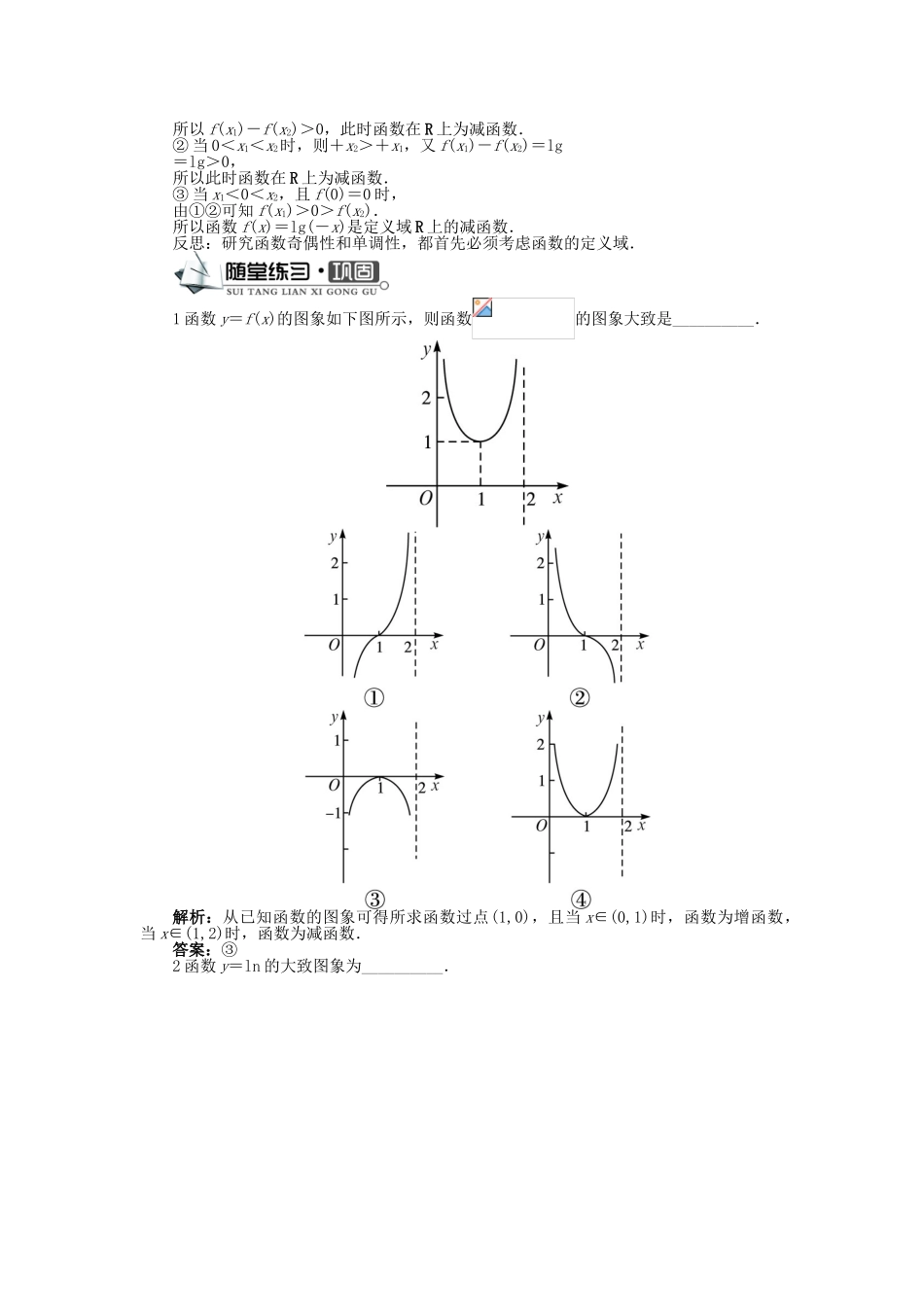
第 2 课时 对数函数的图象与性质通过对数函数的图象及其变换,观察发现对数函数的性质,提高识图能力.对数函数 y=logax(a>1)与指数函数 y=ax(a>1)的性质比较函数y=axy=logax图象性质定义域 R定义域(0 ,+∞ ) 值域(0 ,+∞ ) 值域 R过定点(0,1)过定点(1,0)当 x>0 时,y > 1 ;当 x<0 时,0 < y < 1 当 x>1 时,y > 0 ;当 0<x<1 时,y < 0 在 R 上是增函数在(0,+∞)上是增函数【做一做 1】将指数函数 f(x)=3x的图象沿直线 y=x 翻折后,可得函数__________的图象.答案:y=log3x【做一做 2】将对数函数 y=log2x 的图象向右平移 1 个单位长度后可得函数__________的图象.答案:y=log2(x-1)不同底数的图象之间的变化趋势是怎样的?剖析:由于对数函数 y=logax 的图象与直线 y=1 交于点(a,1)(如图 1 所示),所以对数函数 y=logax 的图象在 x 轴上方,从左到右对应的底数由小到大依次递增;由于对数函数 y=logax 的图象与直线 y=-1 交于点(如图 2 所示),所以对数函数 y=logax 的图象在 x 轴下方,从左到右对应的底数由大到小依次递减. 图 1 图 2题型一 对数函数的图象及变换【例 1】作出函数 y=|log2(x+1)|+2 的图象.解:作复合函数的图象问题,可先考虑它的基本函数的图象,然后作适当的变换完成.先作 y=log2x 的图象―——―→y=log2(x+1)―————————―→y=|log2(x+1)|―————————―→y=|log2(x+1)|+2.如图所示.反思:利用函数图象的三大基本变换平移变换、对称变换、伸缩变换是作复合函数图象的基本途径.本题使用了平移和对称两种方法,在平移中要注意“上、下”和“左、右”与 x,y 的关系;对称变换要注意与 x 轴和 y 轴的关系.题型二 对数函数的性质【例 2】已知函数 f(x)=lg |x|.(1)判断函数 f(x)的奇偶性;(2)画出函数 f(x)的图象的草图;(3)求函数 f(x)的单调递减区间.分析:(1)确定函数的定义域,判断 f(x)和 f(-x)的关系;(2)函数 f(x)的图象关于 y轴对称,利用变换作图画出草图;(3)由图象观察出单调递增区间,再用定义证明.解:(1)要使函数有意义,x 的取值需满足|x|>0,解得 x≠0,即函数的定义域是(-∞,0)∪(0,+∞),f(-x)=lg |-x|=lg |x|=f(x),所以函数 f(x)是偶函数.(2)由于函数 f(x)是偶函数,则其图象关于 y 轴对称,将函数 y=lg x ...