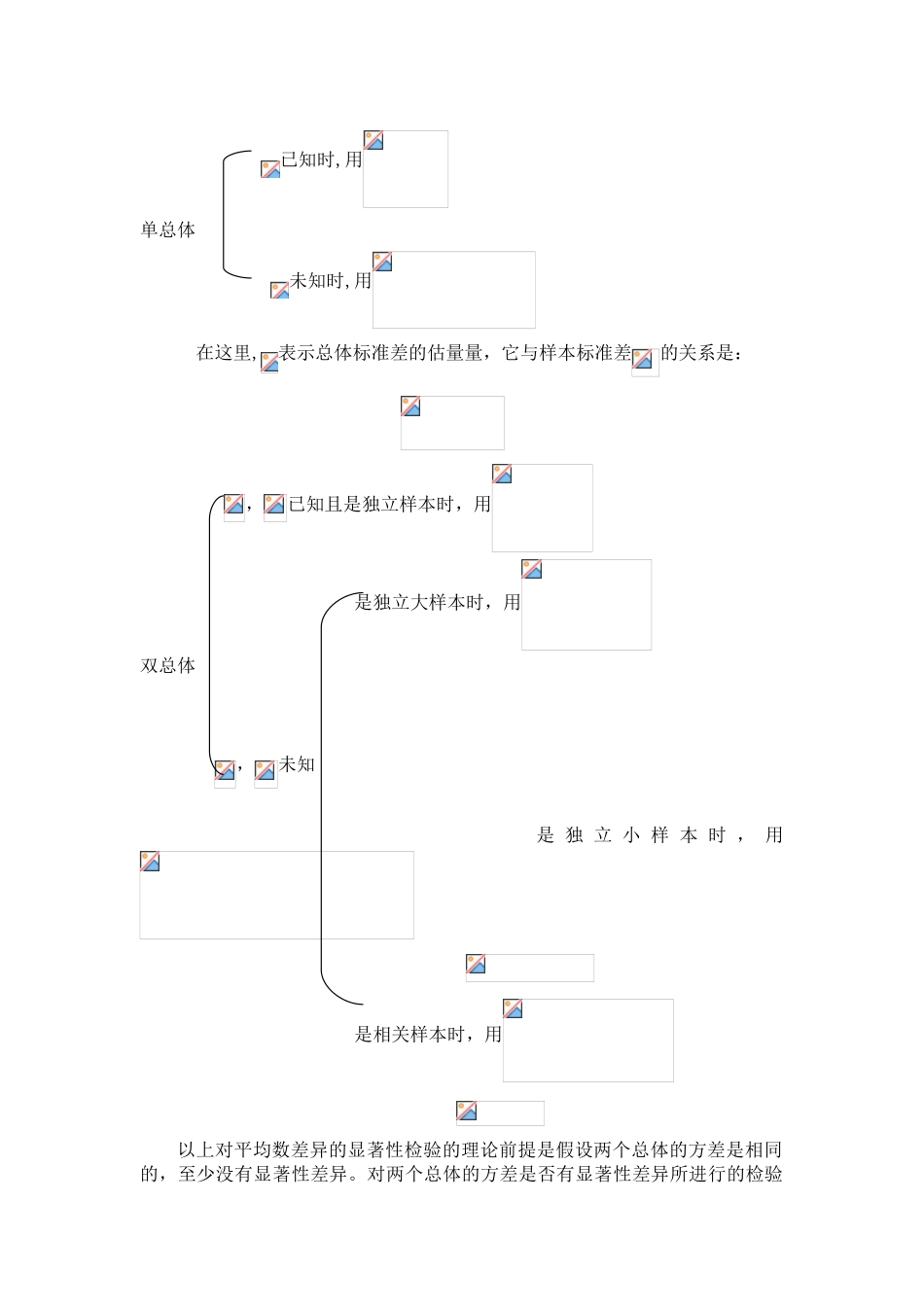
T 检验 F 检验及公式(一) 检验当总体呈正态分布,假如总体标准差未知,而且样本容量<30,那么这时一切可能的样本平均数与总体平均数的离差统计量呈 分布。检验是用 分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著. 检验分为单总体 检验和双总体 检验。1。单总体 检验单总体 检验是检验一个样本平均数与一已知的总体平均数的差异是否显著.当总体分布是正态分布,如总体标准差未知且样本容量<30,那么样本平均数与总体平均数的离差统计量呈 分布。检验统计量为: 。假如样本是属于大样本(>30)也可写成: .在这里, 为样本平均数与总体平均数的离差统计量; 为样本平均数; 为总体平均数; 为样本标准差; 为样本容量。例:某校二年级学生期中英语考试成绩,其平均分数为 73 分,标准差为 17分,期末考试后,随机抽取 20 人的英语成绩,其平均分数为 79.2 分。问二年级学生的英语成绩是否有显著性进步?检验步骤如下:第一步 建立原假设=73第二步 计算 值 第三步 推断因 为 , 以 0 。 05 为 显 著 性 水 平 ,, 查值 表 , 临 界 值,而样本离差的1。63 小与临界值 2。093。所以,接受原假设,即进步不显著。2.双总体 检验双总体 检验是检验两个样本平均数与其各自所代表的总体的差异是否显著.双总体 检验又分为两种情况,一是相关样本平均数差异的显著性检验,用于检验匹配而成的两组被试获得的数据或同组被试在不同条件下所获得的数据的差异性,这两种情况组成的样本即为相关样本。二是独立样本平均数的显著性检验。各实验处理组之间毫无相关存在,即为独立样本。该检验用于检验两组非相关样本被试所获得的数据的差异性。现以相关检验为例,说明检验方法。因为独立样本平均数差异的显著性检验完全类似,只不过。相关样本的 检验公式为: 。在这里,,分别为两样本平均数; ,分别为两样本方差; 为相关样本的相关系数。例:在小学三年级学生中随机抽取 10 名学生,在学期初和学期末分别进行了两次推理能力测验,成绩分别为 79.5 和 72 分,标准差分别为 9.124,9。940.问两次测验成绩是否有显著地差异?检验步骤为:第一步 建立原假设=第二步 计算 值==3.459。第三步 推断根据自由度,查 值表,.由于实际计算出来的=3。495〉3.250=,则,故拒绝原假设.结论为:两次测验成绩有及其显著地差异.由以上可以看出,对平均数差异显著性检验比较复杂,究竟使用检验还是...