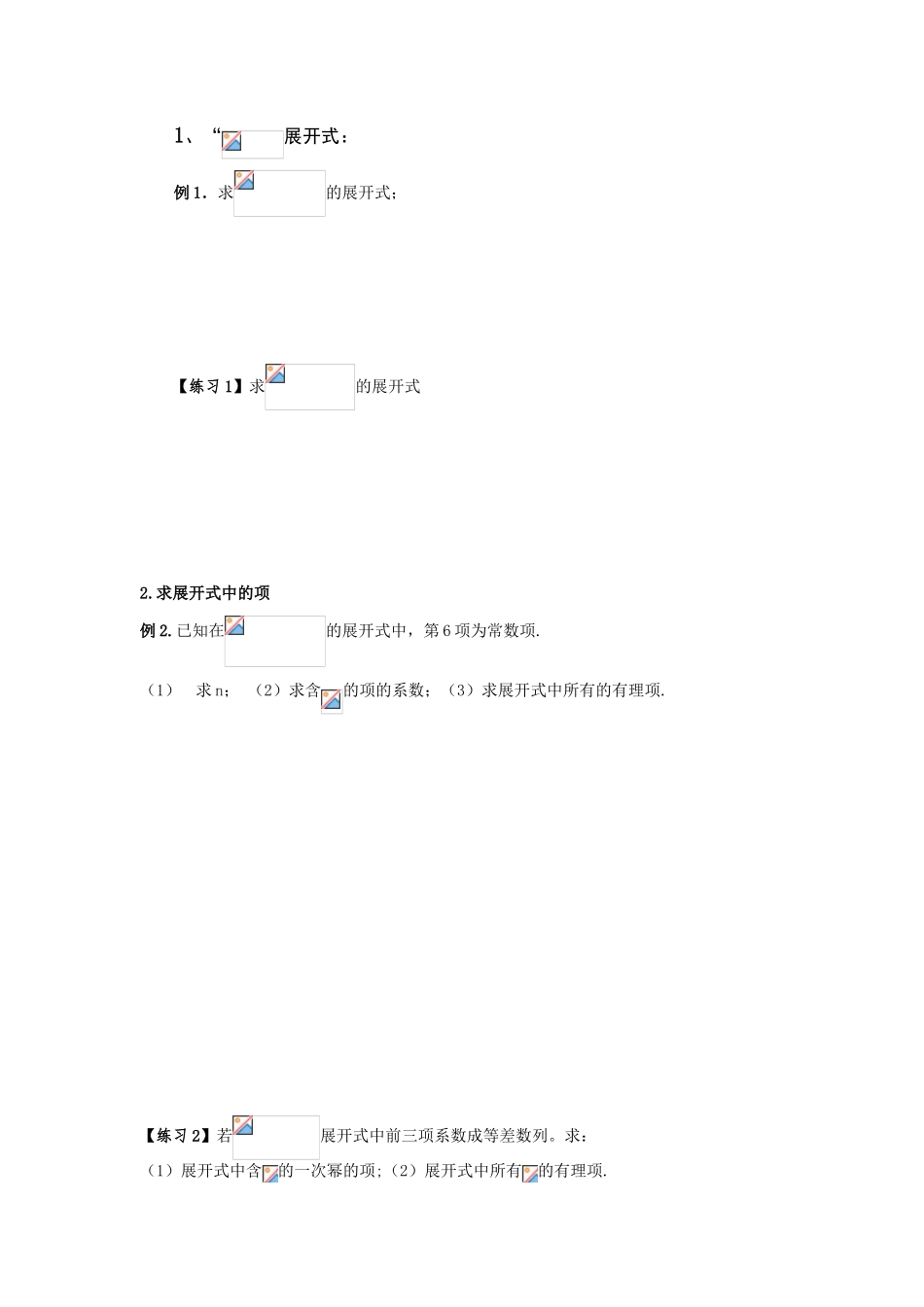
二项式定理二项式知识回顾1. 二项式定理,以上展开式共 n+1 项,其中叫做二项式系数,叫做二项展开式的通项。(请同学完成下列二项展开式), ① ②① 式中分别令 x=1 和 x=—1,则可以得到 ,即二项式系数和等于;偶数项二项式系数和等于奇数项二项式系数和,即② 式中令 x=1 则可以得到二项展开式的各项系数和。2. 二项式系数的性质(1)对称性:与首末两端等距离的两个二项式系数相等,即.(2)二项式系数增减性与最大值:当时,二项式系数是递增的;当时,二项式系数是递减的.当 n 是偶数时,中间一项取得最大值。当 n 是奇数时,中间两项和相等,且同时取得最大值。3 。 二 项 展 开 式 的 系 数 a0,a1 , a2 , a3 , … , an 的 性 质 : f(x)= a0+a1x+a2x2+a3x3……+anxn⑴ a0+a1+a2+a3……+an=f(1) ⑵ a0—a1+a2-a3……+(-1)nan=f(-1)⑶ a0+a2+a4+a6……= ⑷ a1+a3+a5+a7……= 经典例题1、“展开式:例 1.求的展开式;【练习 1】求的展开式2.求展开式中的项例 2.已知在的展开式中,第 6 项为常数项.(1)求 n; (2)求含的项的系数;(3)求展开式中所有的有理项.【练习 2】若展开式中前三项系数成等差数列。求:(1)展开式中含的一次幂的项;(2)展开式中所有的有理项.3.二项展开式中的系数例 3.已知的展开式的二项式系数和比的展开式的二项式系数和大992,求的展开式中:(1)二项式系数最大的项;(2)系数的绝对值最大的项[练习 3]已知的展开式中的第五项的系数与第三项的系数之比是 10:1。(1)求展开式中含的项;(2)求展开式中系数最大的项和二项式系数最大的项。4、求两个二项式乘积的展开式指定幂的系数 例 4.的展开式中,项的系数是 ; 5、求可化为二项式的三项展开式中指定幂的系数例 5(04 安徽改编)的展开式中,常数项是 ; 6、求中间项例 6 求(的展开式的中间项;例 7 的展开式中有理项共有 项;8、求系数最大或最小项(1)特别的系数最大或最小问题例 8(00 上海)在二项式的展开式中,系数最小的项的系数是 ;(2)一般的系数最大或最小问题 例 9 求展开式中系数最大的项;(3)系数绝对值最大的项例 10 在(的展开式中,系数绝对值最大项是 ;9、利用“赋值法”及二项式性质 3 求部分项系数,二项式系数和 例 11 . 若, 则的 值 为 ;【练习 1】若, 则 ;【练习 2】设, 则 ; 【练习 3】展开式中的系数是 ;