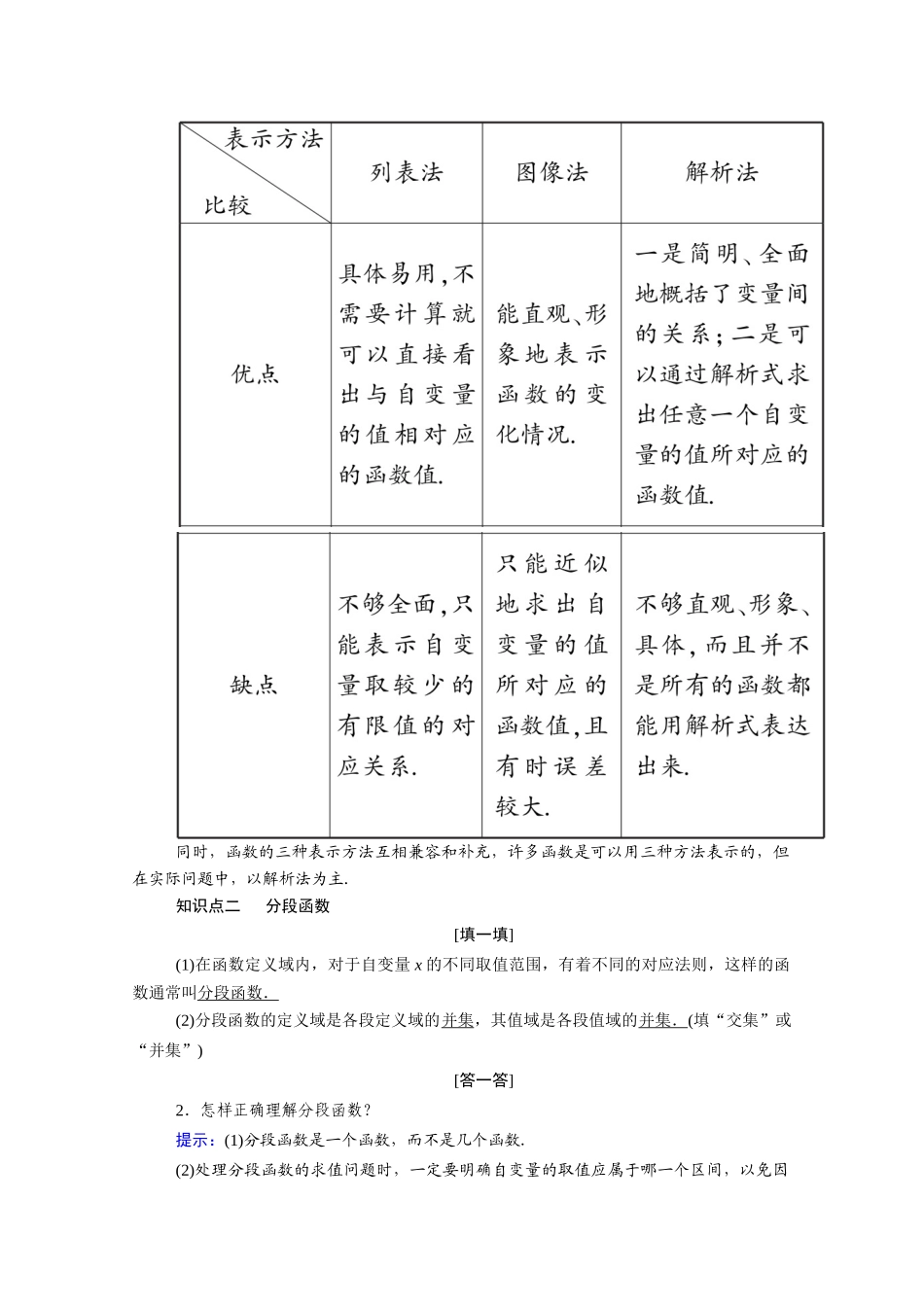
2.2 函数的表示法知识点一 函数的表示法 [填一填] [答一答]1.函数三种表示方法各有哪些优缺点?提示:同时,函数的三种表示方法互相兼容和补充,许多函数是可以用三种方法表示的,但在实际问题中,以解析法为主.知识点二 分段函数 [填一填](1)在函数定义域内,对于自变量 x 的不同取值范围,有着不同的对应法则,这样的函数通常叫分段函数.(2)分段函数的定义域是各段定义域的并集,其值域是各段值域的并集.(填“交集”或“并集”)[答一答]2.怎样正确理解分段函数?提示:(1)分段函数是一个函数,而不是几个函数.(2)处理分段函数的求值问题时,一定要明确自变量的取值应属于哪一个区间,以免因误用法则造成错误结果.(3)分段函数的定义域是各段“定义域”的并集,其值域是各段“值域”的并集.(4)分段函数的图像应分段来作,特别注意各段的自变量取区间端点处时函数值的取值情况,以决定这些点的虚实情况.3.如何准确地作出函数的图像?提示:(1)作函数图像的基本方法:描点作图法:其步骤是:列表、描点、连线成图.此法应先了解函数图像的特点,再列表描点,避免盲目性.(2)检验一个图像 F 是否为函数 y=f(x)的图像应满足两点:① 图像 F 上任一点的坐标(x,y)都满足 y=f(x)关系式;② 满足 y=f(x)关系式的点(x,y)都在图像 F 上.1.三种表示方法的适用范围(1)列表法适用于定义域是有限集的情形.(2)图像法适用于任何函数.(3)解析法适用于对应法则可以用一个数学式子表示的情形.2.函数图像与其解析式的关系(1)函数图像是其解析式的直观反映.用图像法表示函数可以化抽象为直观,较形象地反映出函数关系变化的趋势,把抽象的函数概念形象化.(2)函数图像与其解析式的对应性.函数图像是解析式中自变量与其函数值对应点集合的直观反映,需要注意的是从函数图像上一般只能得到近似的数量关系,但通过解析式可以画出准确的图像.3.对分段函数的理解(1)分段函数是一个函数而不是几个函数;分段函数的定义域、值域分别为各段上定义域与值域的并集.(2)分段函数的“段”可以是等长的也可以是不等长的.(3)写分段函数的定义域时区间端点要做到不重不漏.(4)处理分段函数问题时,要首先确定自变量的取值属于哪一个范围,然后选取相应的对应法则.类型一 列表法表示函数 【例 1】 试用列表法表示 0°,30°,45°,60°,90°角的正弦值、余弦值之间的函数关系.【思路探究】 只需列出自变量(角的度数)与对应函数...