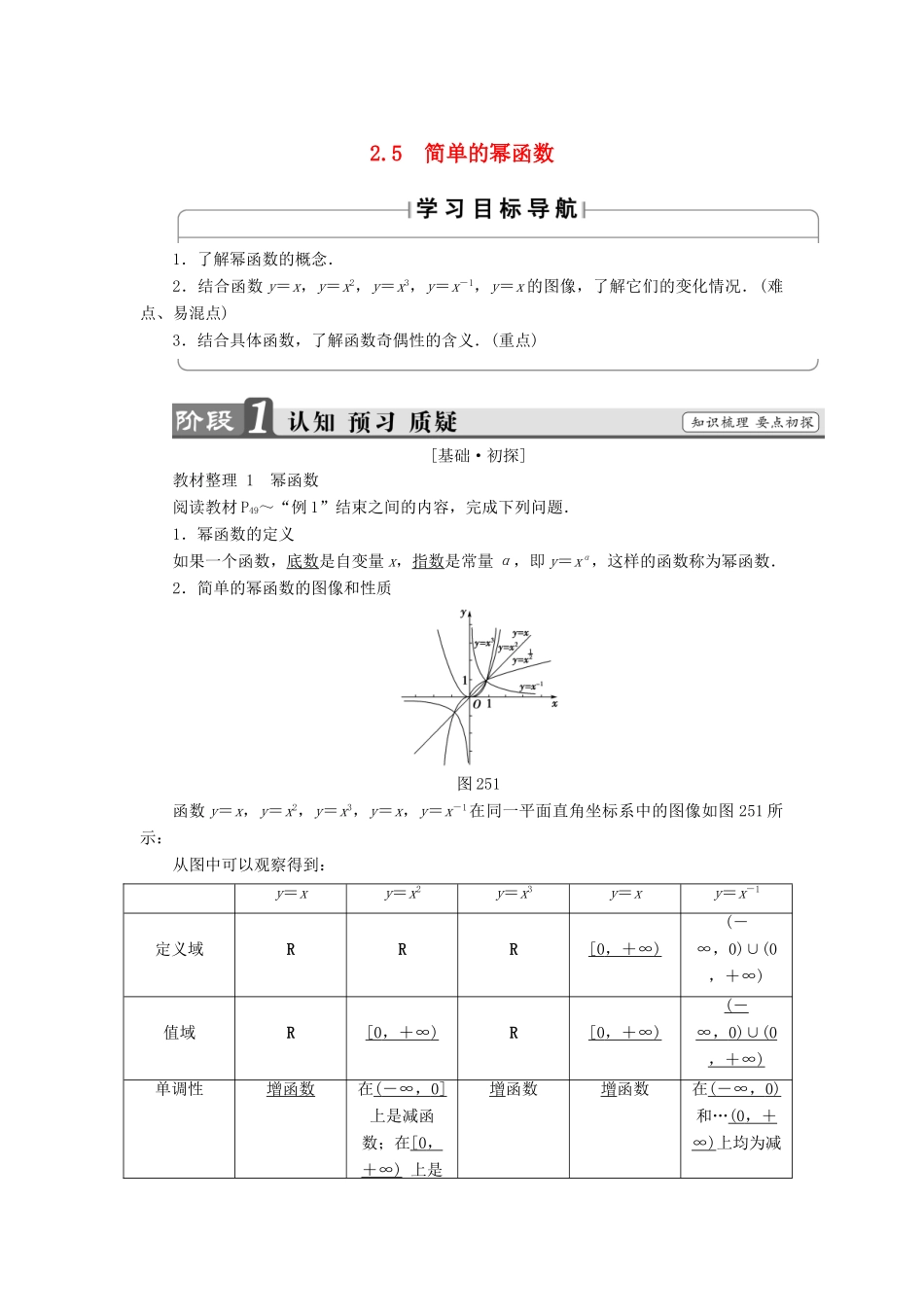
2.5 简单的幂函数1.了解幂函数的概念.2.结合函数 y=x,y=x2,y=x3,y=x-1,y=x 的图像,了解它们的变化情况.(难点、易混点)3.结合具体函数,了解函数奇偶性的含义.(重点)[基础·初探]教材整理 1 幂函数阅读教材 P49~“例 1”结束之间的内容,完成下列问题.1.幂函数的定义如果一个函数,底数是自变量 x,指数是常量 α,即 y=xα,这样的函数称为幂函数.2.简单的幂函数的图像和性质图 251函数 y=x,y=x2,y=x3,y=x,y=x-1在同一平面直角坐标系中的图像如图 251 所示:从图中可以观察得到:y=xy=x2y=x3y=xy=x-1定义域RRR[0 ,+∞ ) (-∞,0)∪(0,+∞)值域R[0 ,+∞ ) R[0 ,+∞ ) ( - ∞, 0)∪(0 ,+∞ ) 单调性增函数在( -∞, 0] 上是减函数;在[0 , +∞ ) 上是增函数增函数在( -∞, 0) 和…(0 ,+ ∞ ) 上均为减增函数函数定点函数图像均过点(1,1) 下列函数中是幂函数的是( )①y=;② y=axm(a,m 为非零常数,且 a≠1);③ y=x+x4;④ y=xn;⑤ y=(x-6)3;⑥ y=8x2;⑦ y=x2+x;⑧ y=1.A.①②③⑧ B.①④C.③④⑤⑥ D.②④⑦【解析】 由幂函数的定义:形如 y=xa(a∈R)的函数才是幂函数,则 y==x-3,y=xn是幂函数.【答案】 B教材整理 2 函数的奇偶性阅读教材 P49从“可以看出”~P50“练习”以上的有关内容,完成下列问题.1.(1)图像奇函数的图像偶函数.(2)解析式奇函数f(-x)=- f ( x ) . 偶函数f(-x)=f(x).2.奇偶性当一个函数是奇函数或偶函数时,称该函数具有奇偶性. 判断(正确的打“√”,错误的打“×”)(1)奇函数的图像一定过原点.( )(2)定义在 R 上的函数 f(x),若存在 x0,使 f(-x0)=f(x0),则函数 f(x)为偶函数.( )(3)函数 y=x2,x∈(-1,1]是偶函数.( )【答案】 (1)× (2)× (3)×[小组合作型]幂函数的概念 函数 f(x)=(m2-m-1)xm2+m-3 是幂函数,且当 x∈(0,+∞)时,f(x)是增加的,求 f(x)的解析式.【精彩点拨】 先由 m2-m-1=1 求出 m 的值,再代入到 m2+m-3 中,找到满足x∈(0,+∞)时,f(x)是增加的 m 的值.【尝试解答】 根据幂函数定义得,m2-m-1=1,解得 m=2 或 m=-1.当 m=2 时,f(x)=x3在(0,+∞)是增加的,符合要求;当 m=-1 时,f(x)=x-3在(0,+∞)上是减少的,不符合要求.因此,f(x)=x3.1.形...