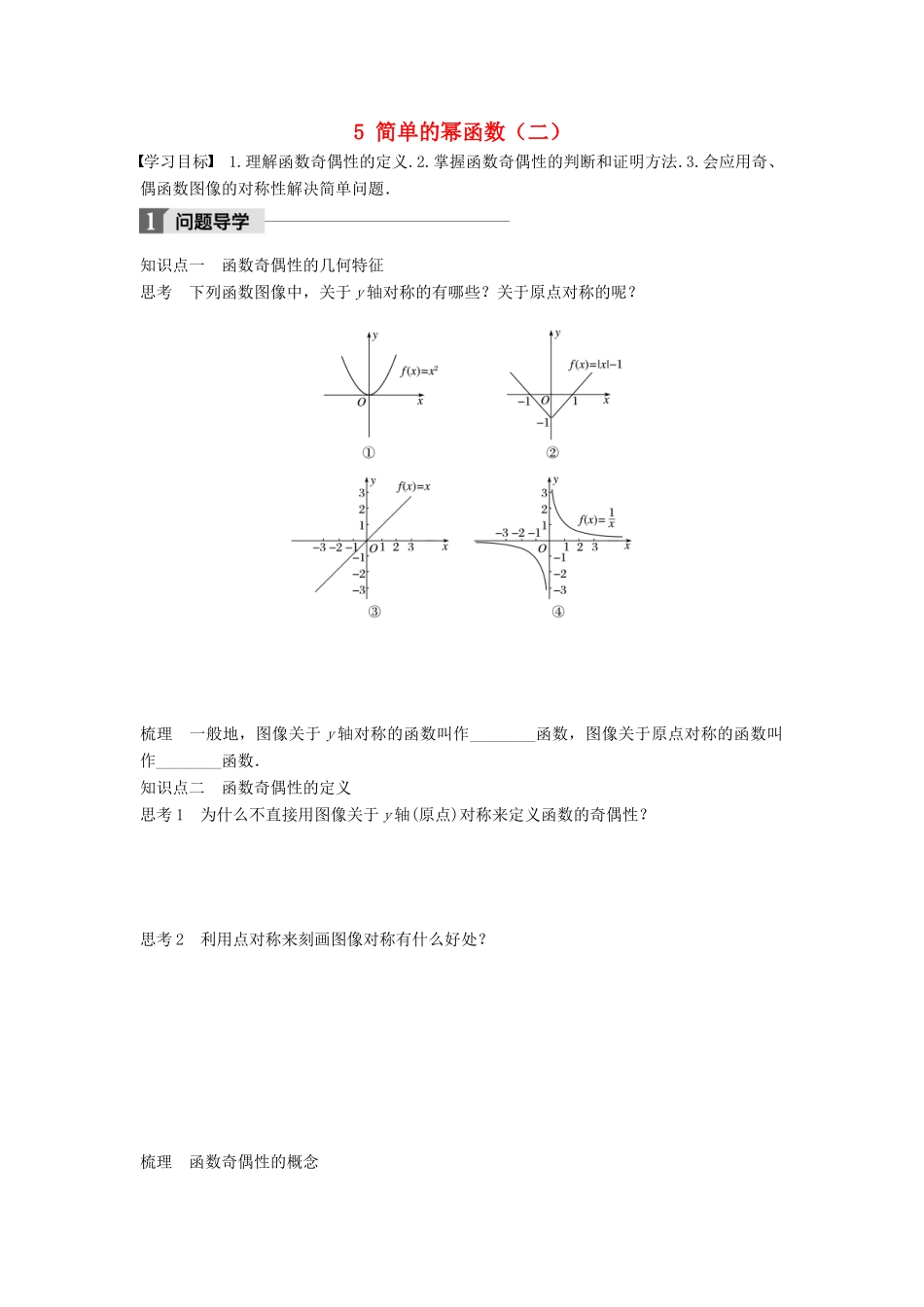
5 简单的幂函数(二)学习目标 1.理解函数奇偶性的定义.2.掌握函数奇偶性的判断和证明方法.3.会应用奇、偶函数图像的对称性解决简单问题.知识点一 函数奇偶性的几何特征思考 下列函数图像中,关于 y 轴对称的有哪些?关于原点对称的呢? 梳理 一般地,图像关于 y 轴对称的函数叫作________函数,图像关于原点对称的函数叫作________函数.知识点二 函数奇偶性的定义思考 1 为什么不直接用图像关于 y 轴(原点)对称来定义函数的奇偶性? 思考 2 利用点对称来刻画图像对称有什么好处? 梳理 函数奇偶性的概念(1)偶函数:如果对于函数 f(x)的定义域内任意一个 x,都有________________,那么函数f(x)就叫作偶函数.其实质是函数 f(x)上任一点(x,f(x))关于 y 轴的对称点(-x,f(x))也在 f(x)图像上.(2)奇函数:如果对于函数 f(x)的定义域内任意一个 x,都有________________,那么函数f(x)就叫作奇函数.其实质是函数 f(x)上任一点(x,f(x))关于原点的对称点(-x,-f(x))也在 f(x)图像上.(3)由函数奇偶性定义,对于定义域内任一元素 x,其相反数-x 必须也在定义域内,所以判断函数奇偶性要注意定义域优先原则,即首先要看定义域是否关于原点对称.知识点三 奇偶性与单调性思考 观察偶函数 y=x2与奇函数 y=在(-∞,0)和(0,+∞)上的单调性,你有何猜想? 梳理 (1)若奇函数 f(x)在[a,b]上是增函数,且有最大值 M,则 f(x)在[-b,-a]上是________函数,且有最小值________.(2)若偶函数 f(x)在(-∞,0)上是减函数,则 f(x)在(0,+∞)上是__________.(3)知道了函数的奇偶性,我们可以先研究函数的一半,再利用对称性了解其另一半,从而减少工作量.类型一 判断函数的奇偶性例 1 判断并证明下列函数的奇偶性:(1)f(x)=;(2)f(x)=(x+1)(x-1);(3)f(x)=+. 反思与感悟 利用定义法判断函数是否具有奇偶性时,首先应看函数定义域是否关于原点对称,即对于定义域内的任意一个 x,则-x 也一定属于定义域.跟踪训练 1 判断并证明下列函数的奇偶性:(1)f(x)=(x-2) ;(2)f(x)=x|x|;(3)f(x),g(x)是定义在 R 上的奇函数,试判断 y=f(x)+g(x),y=f(x)g(x),y=f[g(x)]的奇偶性. 类型二 奇偶性的应用例 2 定义在 R 上的奇函数 f(x)在[0,+∞)上的图像如图所示.(1)画出 f(x)的图像;(2)解不等式 xf(x)>0.引申探究把例 2 中的“奇函数”改为“偶函数”,重做该题. ...