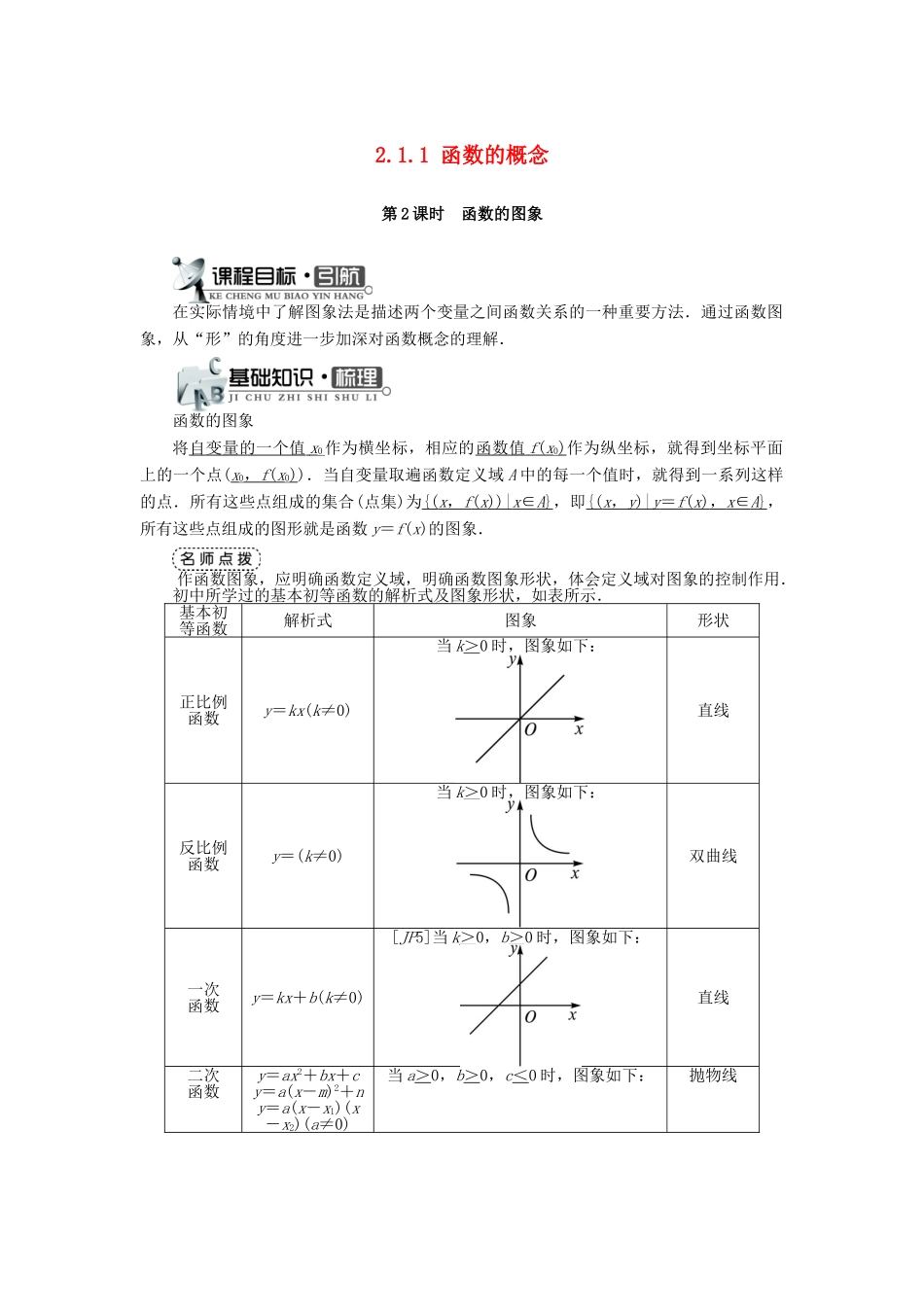
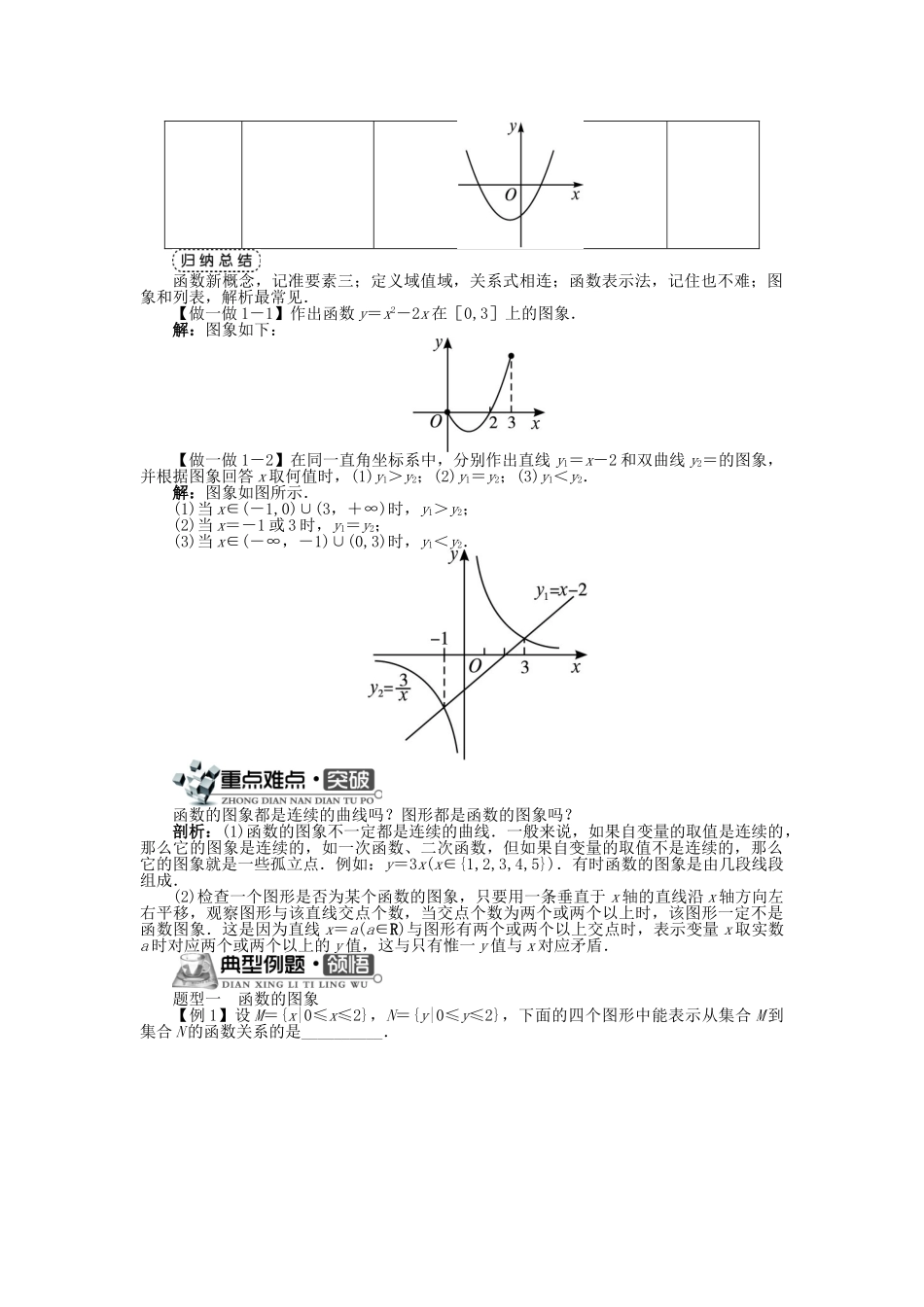
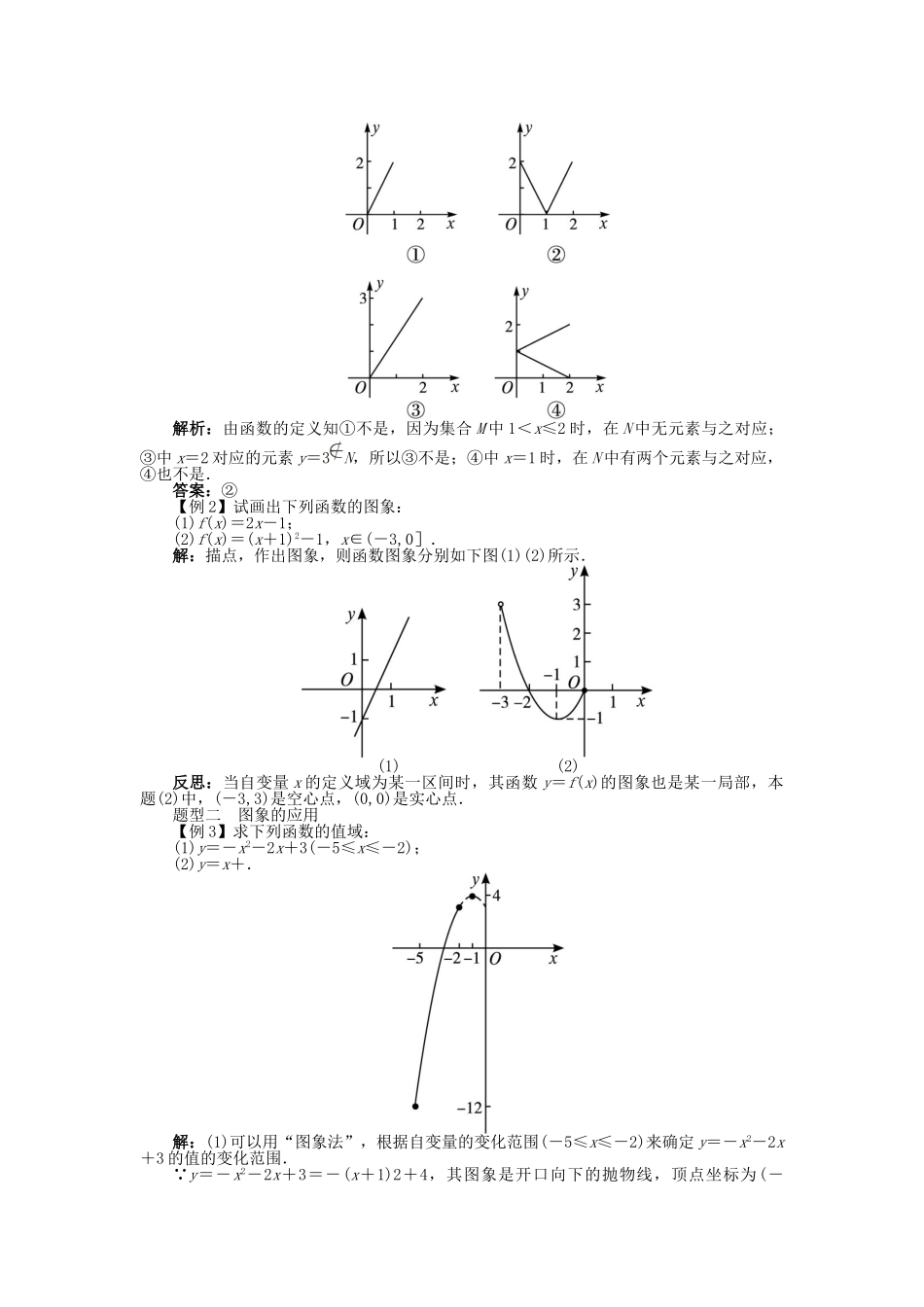
2.1.1 函数的概念第 2 课时 函数的图象在实际情境中了解图象法是描述两个变量之间函数关系的一种重要方法.通过函数图象,从“形”的角度进一步加深对函数概念的理解.函数的图象将自变量的一个值 x 0 作为横坐标,相应的函数值 f ( x 0)作为纵坐标,就得到坐标平面上的一个点(x0, f ( x 0)).当自变量取遍函数定义域 A 中的每一个值时,就得到一系列这样的点.所有这些点组成的集合(点集)为{( x , f ( x ))| x ∈ A } ,即{( x , y )| y = f ( x ) , x ∈ A } ,所有这些点组成的图形就是函数 y=f(x)的图象.作函数图象,应明确函数定义域,明确函数图象形状,体会定义域对图象的控制作用.初中所学过的基本初等函数的解析式及图象形状,如表所示.基本初等函数解析式图象形状正比例函数y=kx(k≠0)当 k>0 时,图象如下:直线反比例函数y=(k≠0)当 k>0 时,图象如下:双曲线一次函数y=kx+b(k≠0)[JP5]当 k>0,b>0 时,图象如下:直线二次函数y=ax2+bx+cy=a(x-m)2+ny=a(x-x1)(x-x2)(a≠0)当 a>0,b>0,c<0 时,图象如下:抛物线函数新概念,记准要素三;定义域值域,关系式相连;函数表示法,记住也不难;图象和列表,解析最常见.【做一做 1-1】作出函数 y=x2-2x 在[0,3]上的图象.解:图象如下:【做一做 1-2】在同一直角坐标系中,分别作出直线 y1=x-2 和双曲线 y2=的图象,并根据图象回答 x 取何值时,(1)y1>y2;(2)y1=y2;(3)y1<y2.解:图象如图所示.(1)当 x∈(-1,0)∪(3,+∞)时,y1>y2;(2)当 x=-1 或 3 时,y1=y2;(3)当 x∈(-∞,-1)∪(0,3)时,y1<y2.函数的图象都是连续的曲线吗?图形都是函数的图象吗?剖析:(1)函数的图象不一定都是连续的曲线.一般来说,如果自变量的取值是连续的,那么它的图象是连续的,如一次函数、二次函数,但如果自变量的取值不是连续的,那么它的图象就是一些孤立点.例如:y=3x(x∈{1,2,3,4,5}).有时函数的图象是由几段线段组成.(2)检查一个图形是否为某个函数的图象,只要用一条垂直于 x 轴的直线沿 x 轴方向左右平移,观察图形与该直线交点个数,当交点个数为两个或两个以上时,该图形一定不是函数图象.这是因为直线 x=a(a∈R)与图形有两个或两个以上交点时,表示变量 x 取实数a 时对应两个或两个以上的 y 值,这与只有惟一 y 值与 x 对应矛盾.题型一 函数...