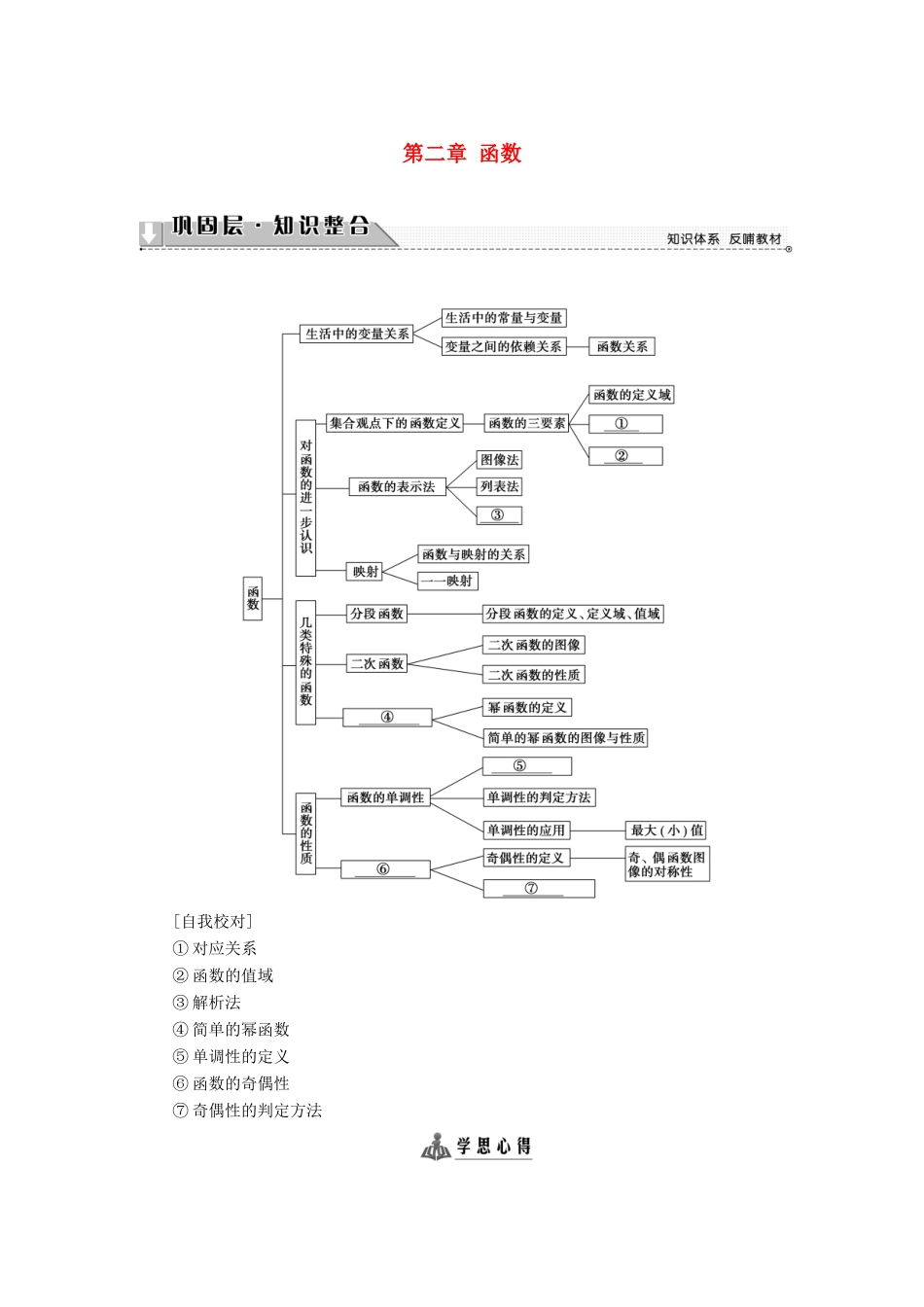
第二章 函数[自我校对]① 对应关系② 函数的值域③ 解析法④ 简单的幂函数⑤ 单调性的定义⑥ 函数的奇偶性⑦ 奇偶性的判定方法 函数的定义域1.已知函数解析式求其定义域,就是求使解析式有意义(分母不为零,偶次根式的被开方数非负等)的自变量的取值范围.2.已知函数 f(x)的定义域为[a,b],求函数 f[φ(x)]的定义域,可解不等式a≤φ(x)≤b 求得;如果已知函数 f[φ(x)]的定义域,可通过求函数 φ(x)的值域,求得函数 f(x)的定义域. (1)若函数 y=的定义域为 R,则实数 a 的取值范围是________.(2)已知函数 f(x)的定义域为[0,1],则函数 f 的定义域为________.【精彩点拨】 (1)对任意 x∈R,都有 ax2+4ax+3≠0 成立,分 a=0,a≠0 两种情况,a≠0 时,Δ<0 即可;(2)由 0≤x-1≤1 解出 x 的范围即为所求.【规范解答】 (1)依题意,x∈R,解析式有意义,即对任意 x∈R,都有 ax2+4ax+3≠0 成立,故方程 ax2+4ax+3=0 无实根.① 当 a=0 时,3≠0 满足要求;② 当 a≠0 时,则有 Δ=16a2-12a<0,即 0<a<时满足要求.综上可知 a∈.(2)由题意知,0≤x-1≤1,解得 2≤x≤4.因此,函数 f 的定义域为[2,4].【答案】 (1) (2)[2,4][再练一题]1.已知函数 f(2x-1)的定义域为[0,1),求 f(1-3x)的定义域. 【导学号:04100036】【解】 f(2x-1)的定义域为[0,1),∴0≤x<1,∴-1≤2x-1<1,∴f(x)的定义域为[-1,1),即-1≤1-3x<1,0<x≤.故函数 f(1-3x)的定义域为.函数的性质 函数的单调性和奇偶性是函数的两个重要的性质:(1)利用函数的单调性,可将函数值之间的关系转化为自变量间的关系进行研究,从而达到化繁为简的目的,特别是比较大小、证明不等式、求值域或最值等方面的应用较为广泛.判定单调性的方法主要有定义法,图像法.(2)利用奇偶函数图像的对称性,可以减少对变量的讨论,常能使求解的问题避免复杂的讨论. 已知函数 f(x)=是奇函数,且 f(2)=.(1)求实数 a,b 的值;(2)判断函数 f(x)在(-∞,-1]上的单调性,并加以证明.【精彩点拨】 (1)利用奇函数定义和 f(2)=,求 a,b 的值;(2)根据单调性的定义证明.【规范解答】 (1) f(x)是奇函数,∴f(-x)=-f(x),∴=-,∴-3x+b=-3x-b,因此 b=-b,即 b=0.又 f(2)=,∴=,∴a=2.(2)由(1)知,f(x)==,f(x)在(-∞,-1]上为增加的.证明:设 x1<x2≤-1,则 f(x...