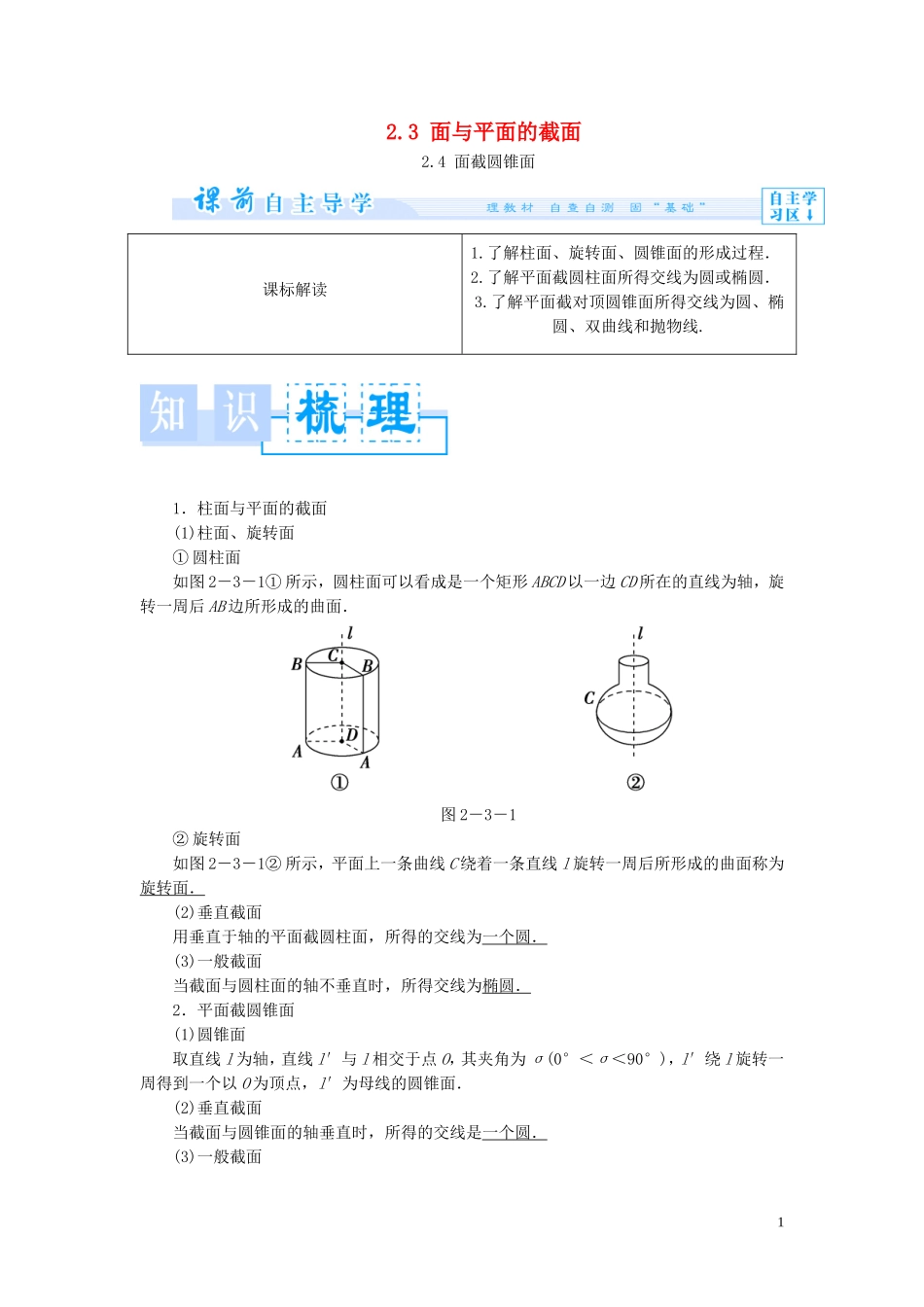
2.3 面与平面的截面2.4 面截圆锥面课标解读1.了解柱面、旋转面、圆锥面的形成过程.2.了解平面截圆柱面所得交线为圆或椭圆.3.了解平面截对顶圆锥面所得交线为圆、椭圆、双曲线和抛物线.1.柱面与平面的截面(1)柱面、旋转面① 圆柱面 如图 2-3-1① 所示,圆柱面可以看成是一个矩形 ABCD 以一边 CD 所在的直线为轴,旋转一周后 AB 边所形成的曲面.图 2-3-1② 旋转面如图 2-3-1② 所示,平面上一条曲线 C 绕着一条直线 l 旋转一周后所形成的曲面称为旋转面.(2)垂直截面用垂直于轴的平面截圆柱面,所得的交线为一个圆.(3)一般截面当截面与圆柱面的轴不垂直时,所得交线为椭圆.2.平面截圆锥面(1)圆锥面取直线 l 为轴,直线 l′与 l 相交于点 O,其夹角为 σ(0°<σ<90°),l′绕 l 旋转一周得到一个以 O 为顶点,l′为母线的圆锥面.(2)垂直截面当截面与圆锥面的轴垂直时,所得的交线是一个圆.(3)一般截面1定理:在空间,直线 l′与 l 相交于点 O,其夹角为 σ,l′绕 l 旋转一周得到以 O 为顶点,l′为母线的圆锥面,任取平面 β,若它与轴 l 的交角为 θ,则① 当 θ>σ 时,平面 β 与圆锥面的交线为椭圆;② 当 θ=σ 时,平面 β 与圆锥面的交线为抛物线;③ 当 θ<σ 时,平面 β 与圆锥面的交线为双曲线.1.平面 β 截圆柱面,β 与圆柱面的轴的夹角 θ 变化,所截出的椭圆有什么变化?【提示】 θ 变化不影响椭圆的短轴,θ 越小,长轴越长,椭圆越扁,离心率越大.2.试研究以过抛物线的焦点的弦为直径的圆与抛物线的准线的位置关系.【提示】 如图,弦 AB 过焦点 F,设其中点为 P,A、B、P 在抛物线准线 l 上的射影分别为 A′、B′、P′,则 PP′为梯形 A′ABB′的中位线,∴PP′=(AA′+BB′),又由抛物线定义可知,AA′+BB′=AF+BF=AB,∴以弦 AB 为直径的圆与 l 相切.3.若平面与圆柱面轴的夹角为 θ,圆柱面的半径为 r,则平面截圆柱面所得的椭圆的长轴长 2a,短轴长 2b,离心率 e 的值如何用 θ、r 表示?【提示】 由两焦球球心距离等于截得椭圆的长轴长,故 2a=,椭圆的短轴长 2b=2r,离心率 e==cos θ.平面与圆柱面交线性质的应用 圆柱的底面半径为 5,高为 5,若一平行于轴的平面截圆柱得一正方形,求轴到截面的距离.【思路探究】 将题目中给出的关系转化为线面关系求解.2【自主解答】 如图所...