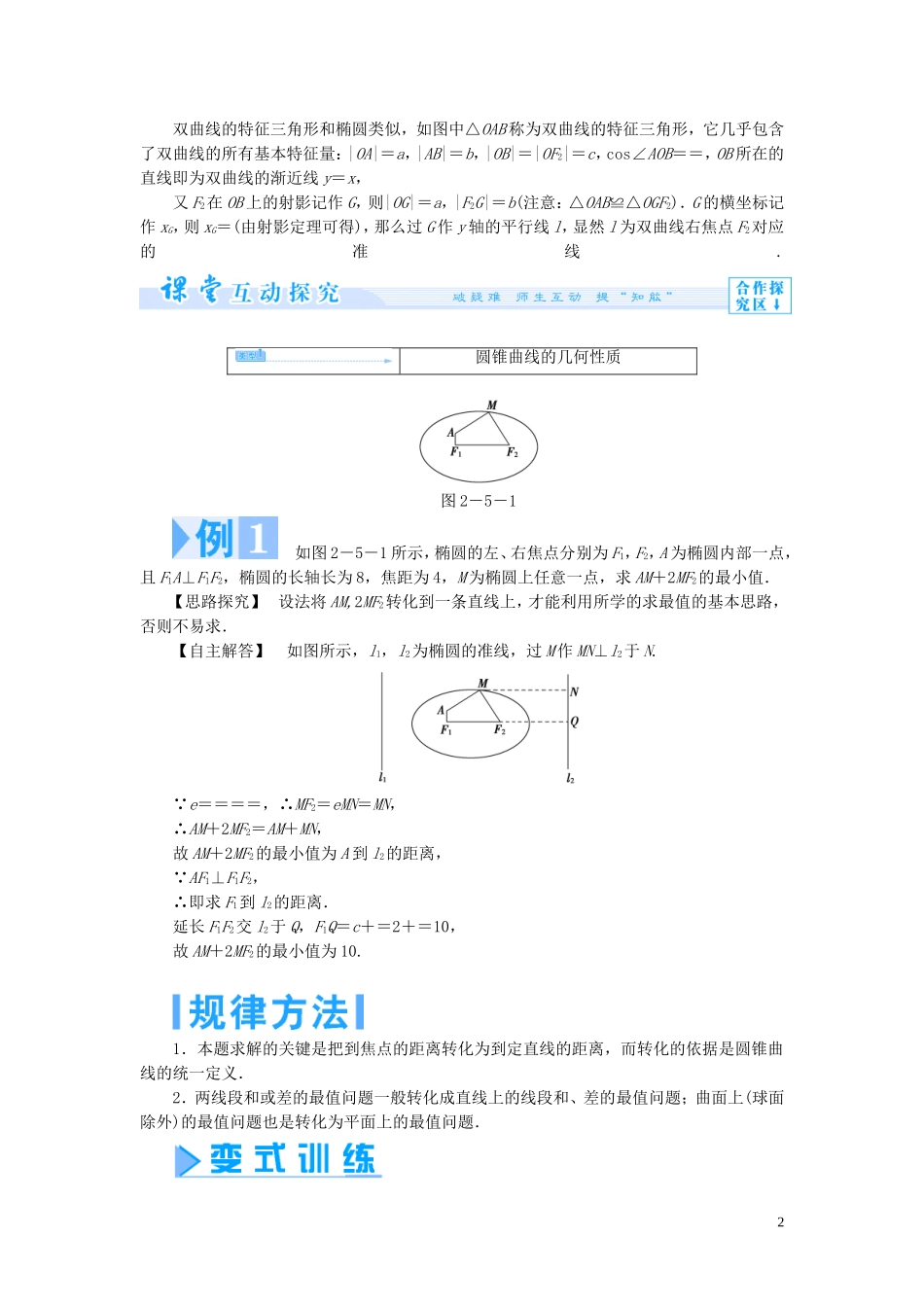
2.5 圆锥曲线的几何性质课标解读1.了解圆锥曲线的形成过程.2.理解圆锥曲线的统一定义.3.能用圆锥曲线的几何性质解决问题.圆锥曲线的统一定义抛物线、椭圆、双曲线都是平面上到定点的距离与到定直线的距离之比为常数 e(离心率)的动点的轨迹,此时定点称为焦点,定直线称为准线.当 e=1 时,轨迹为抛物线;当 0<e<1 时,轨迹为椭圆;当 e>1 时,轨迹为双曲线.1.你能列举几条椭圆的几何性质吗?【提示】 (1)椭圆中有“四线”(两条对称轴、两条准线),“六点”(两个焦点、四个顶点).注意它们之间的位置关系(如准线垂直于长轴所在的直线、焦点在长轴上等)及相互间的距离(如焦点到相应顶点的距离为 a-c,到相应准线的距离为-c 等).(2)设椭圆方程+=1(a>b>0)上任意一点为 P(x,y),则|OP|=== . -a≤x≤a,∴x=0 时,|OP|有最小值 b,这时,P 在短轴端点处;当 x=±a 时,|OP|有最大值 a,这时 P 在长轴端点处.(3)椭圆上任意一点 P(x,y)(y≠0)与两焦点 F1(-c,0),F2(c,0)构成△PF1F2称之为焦点三角形,周长为 2(a+c).(4)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形的边长有 a2=b2+c2.2.由双曲线的特征三角形我们可得到什么?【提示】 1双曲线的特征三角形和椭圆类似,如图中△OAB 称为双曲线的特征三角形,它几乎包含了双曲线的所有基本特征量:|OA|=a,|AB|=b,|OB|=|OF2|=c,cos∠AOB==,OB 所在的直线即为双曲线的渐近线 y=x,又 F2在 OB 上的射影记作 G,则|OG|=a,|F2G|=b(注意:△OAB≌△OGF2).G 的横坐标记作 xG,则 xG=(由射影定理可得),那么过 G 作 y 轴的平行线 l,显然 l 为双曲线右焦点 F2对应的准线.圆锥曲线的几何性质图 2-5-1 如图 2-5-1 所示,椭圆的左、右焦点分别为 F1,F2,A 为椭圆内部一点,且 F1A⊥F1F2,椭圆的长轴长为 8,焦距为 4,M 为椭圆上任意一点,求 AM+2MF2的最小值.【思路探究】 设法将 AM,2MF2转化到一条直线上,才能利用所学的求最值的基本思路,否则不易求.【自主解答】 如图所示,l1,l2为椭圆的准线,过 M 作 MN⊥l2于 N. e====,∴MF2=eMN=MN,∴AM+2MF2=AM+MN,故 AM+2MF2的最小值为 A 到 l2的距离, AF1⊥F1F2,∴即求 F1到 l2的距离.延长 F1F2交 l2于 Q,F1Q=c+=2+=10,故 AM+2MF2的最小值为 10.1.本题求解的关键是把到焦点的距离转化为到定直线的距...