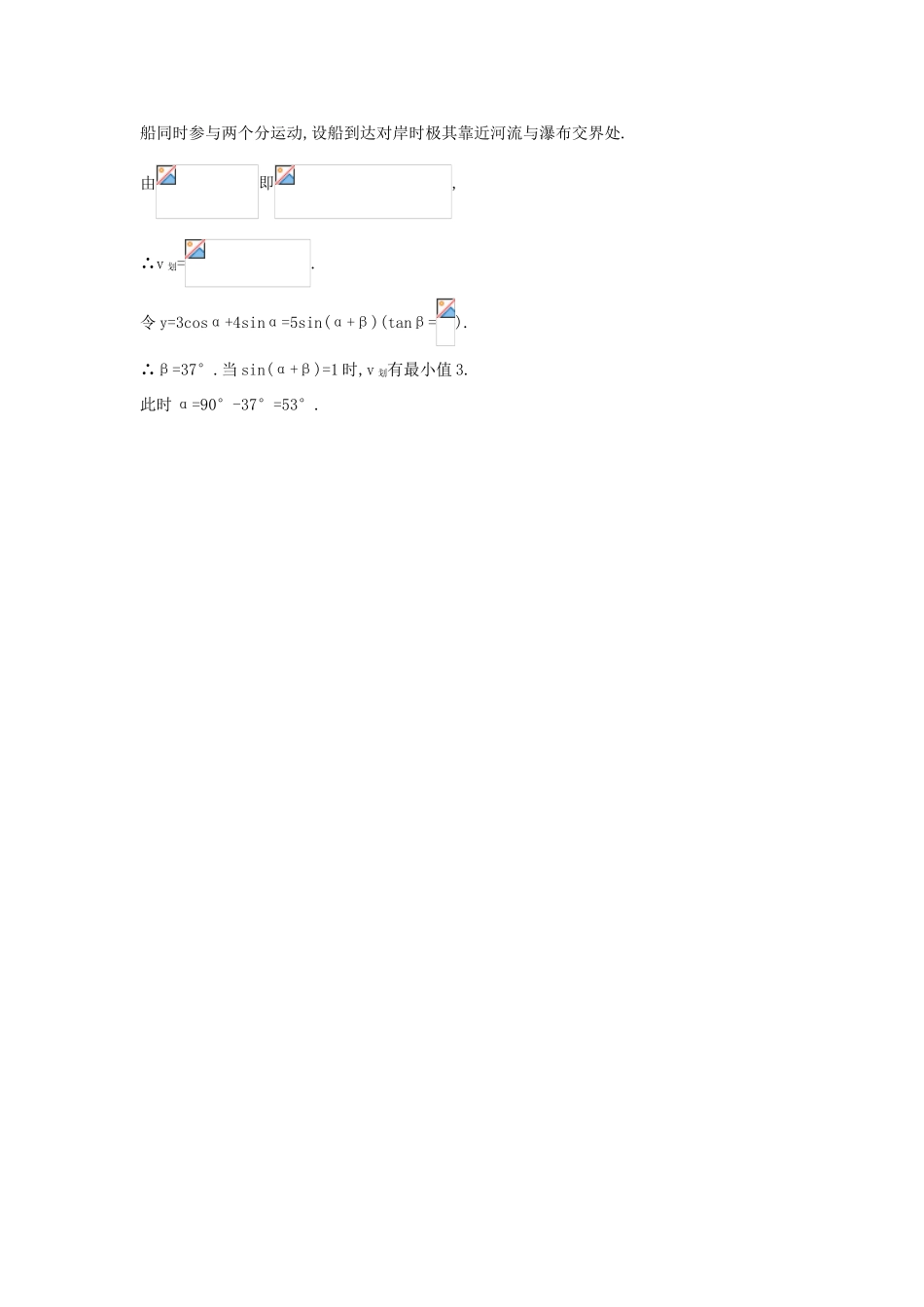
2.5.2 向量在物理中的应用举例互动课堂疏导引导1.力向量 力向量与前面学过的向量不同,它不是自由向量,它不仅包括大小和方向,而且还有作用点.大小相同、方向相同的两个力,如果作用点不同,那么它们是不同的两个力,但力是具有大小和方向的量,在不计作用点的情况下,可利用向量运算法则进行计算.案例 在重 300 N 的物体上系两根绳子,这两根绳子在铅直线的两侧,与铅直线的夹角分别为 30°、60°(如图 2-5-5),求重物平衡时,两根绳子拉力的大小.【探究】注意到两根绳子的夹角为 90°,因此可将问题转化到直角三角形中,作OACB,使∠AOC=30°,∠BOC=60°,∠OAC=90°,||=||·cos30°=N,||=||·sin30°=150 N,||=||=150 N. 图 2-5-52.速度向量 速度向量是具有大小和方向的量,质点在运动中时刻都有对应的速度向量,如东北风 50 m/s,可用图 2-5-6 中有向线段表示.图 2-5-6【规律总结】 (1)力速度、加速度、位移都是向量,向量的加减法即以上向量的合成与分解.(2)动量 mv 是数乘向量.(3)功即力 F 与所产生位移 s 的数量积.(4)学习本节课要注意两个方面的问题:一方面是如何把物理问题转化为数学问题,也就是将物理量之间的关系抽象成数学模型,另一方面就是如何利用建立起来的数学模型解释和回答相应的物理现象.活学巧用1.一条渔船距对岸 4 km,以 2 km/h 的速度向垂直于对岸的方向划去,到达对岸时,船的实际航程为 8 km,求河水的流速.图 2-5-7解析:如图 2-5-7 所示,设河水流速为 v1,实际航向与水流方向的夹角为 α,则 sinα==,所以 α=30°.|v1|=(km/h),即水的流速大小为km/h.2.今有一小船位于 d=60 m 宽的河边 P 处,从这里起,在下游 l=80 m 的 L 处河流变成“飞流直下三千尺”的瀑布,若河水流速方向由上游指向下游(与河岸平行),水速大小为 5 m/s.如图 2-5-8 所示,为使小船能安全渡河,船速不能小于多少?划速最小时划速方向如何?图 2-5-8解析:设该船的划速为 v 划,方向与上游河岸夹角为 α,如图 2-5-9 所示,将 v 划正交分解为v1,v2,则 v1=v 划cosα,v2=v 划sinα.图 2-5-9船同时参与两个分运动,设船到达对岸时极其靠近河流与瀑布交界处.由即,∴v 划=.令 y=3cosα+4sinα=5sin(α+β)(tanβ=).∴β=37°.当 sin(α+β)=1 时,v 划有最小值 3.此时 α=90°-37°=53°.