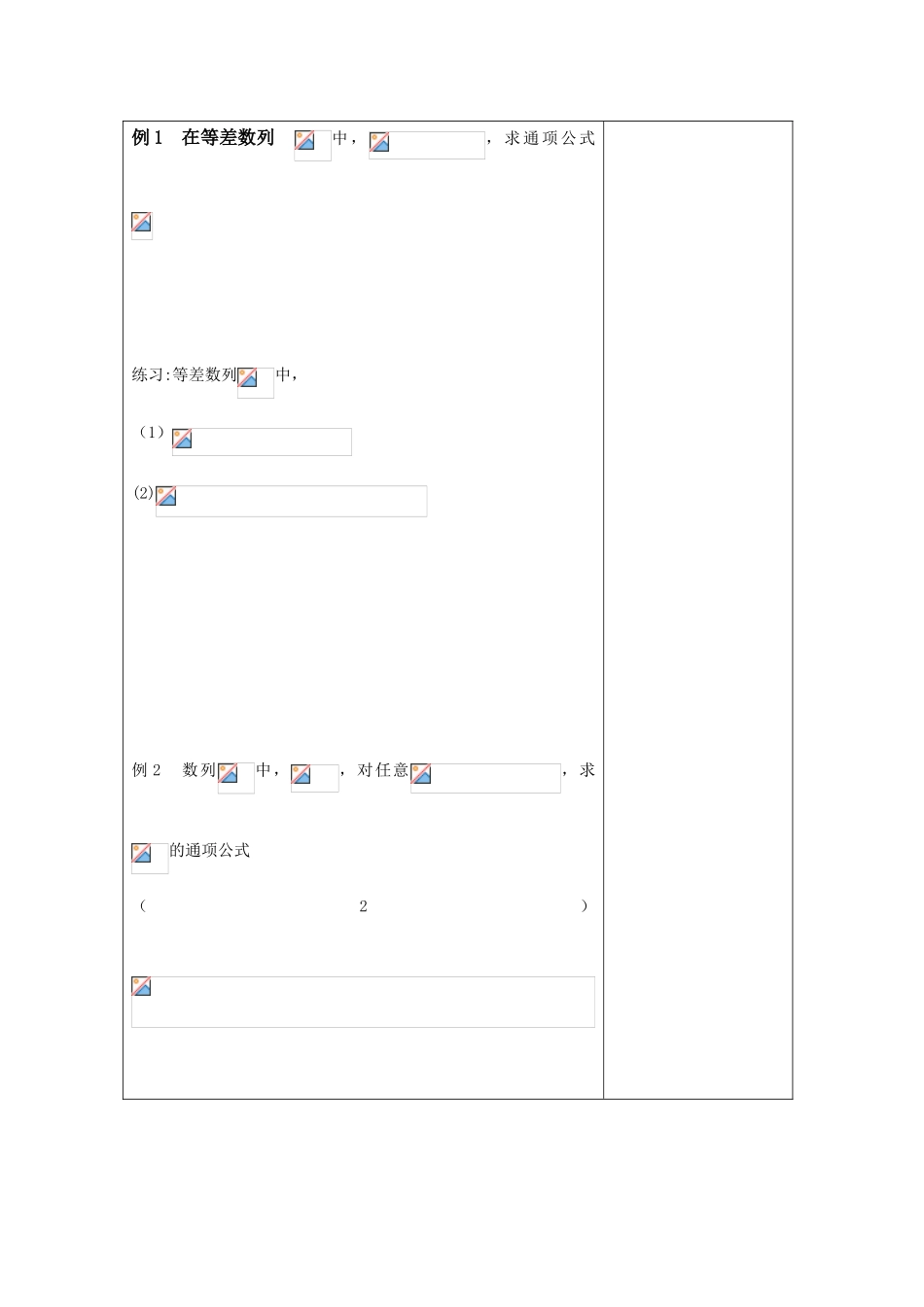
高一数学教学案课题:等差数列的通项公式 时间: 课时数: 1 制卷人:学习目标:等差数列的定义,通项公式,性质的理解与应用教学重点:灵活应用等差数列的定义,性质解题教学难点:教学方法:一、知识预习(重难点、基本概念公式)知识点:1.等差数列的定义2.等差数列的通项公式3.等差中项4.判定等差数列的常用方法5.等差数列的常用性质及证明 二、例题探究例 1 在等差数列中,,求通项公式练习:等差数列中,(1)(2)例 2 数列中,,对任意,求的通项公式(2) 例3 已知的通项公式为(1)p,q 满足什么条件时,是等差数列?(2) 证明:对任意实数 p,q,是等差数列?三、课堂巩固练习1,在等差数列中,(1)若(2)(3)2.等差数列中,四、课堂小结通过本节学习,要求学生掌握等差数列的通项公式,性质及应用。五、课后练习1.m 和 2n 的等差中项是 4,2m 和 n 的等差中项是 5,则 m 和 n 的等差中项是 2.等差数列的第 n+2 项是 ( )3.4.设公差为-2的等差数列,若 5. 中6. 数 列中 ,, 且 对 于 任 意 大 于1的 正 整 数n , 点7.三个数成等差数列,和是 15,平方和 83,求这三个数。8.在数列中,