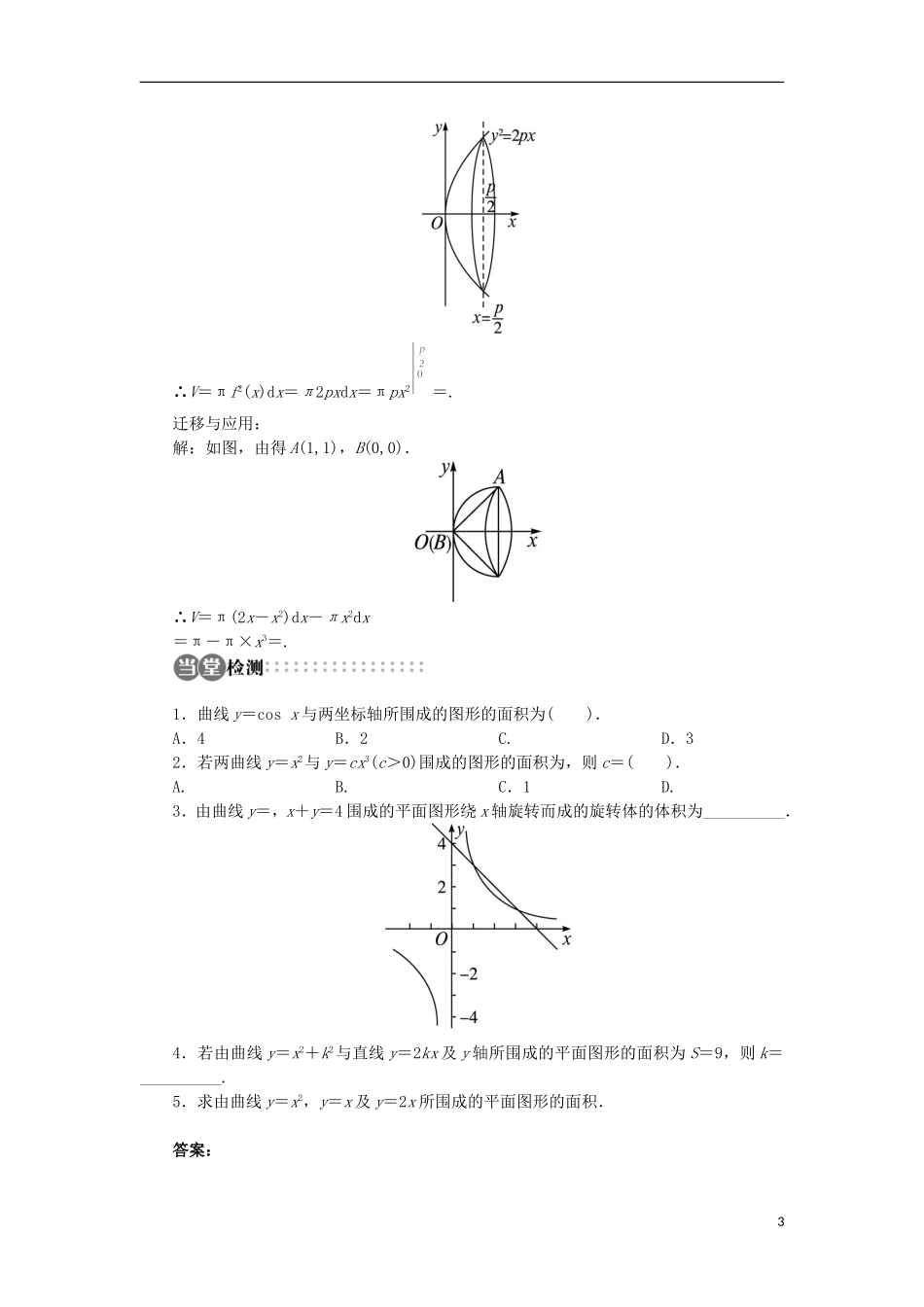
§3 定积分的简单应用学习目标重点难点1.能用求定积分的方法求由已知曲线所围成的平面图形的面积.2.能用求定积分的方法求简单的几何体的体积.重点:平面图形和简单几何体的构成.难点:平面图形的面积和简单几何体的体积的求法.一般地,设由曲线________,________以及直线________,________ 所围成的平面图形(如图)的面积为 S,则:S=________.预习交流议一议:试总结用定积分求曲线围成图形的面积的步骤.答案:预习导引y=f(x) y=g(x) x=a x=b 预习交流:提示:(1)画出图形草图;(2)借助图形直观确定积分变量和被积函数;(3)求出交点的坐标确定积分的上、下限;(4)利用微积分基本定理计算定积分,求出平面图形面积.在预习中还有哪些问题需要你在听课时加以关注?请在下列表格中做个备忘吧!我的学困点我的学疑点一、平面图形的面积求正弦曲线 y=sin x,x∈和直线 x=及 x 轴所围成的平面图形的面积.思路分析:当 x∈[0,π]时,曲线 y=sin x 位于 x 轴的上方,而当 x∈时,曲线位于 x 轴的下方,因此面积应为两部分面积的和.求 y=-x2与 y=x-2 围成的图形的面积 S.1 两条或两条以上曲线围成的图形,一定要确定图形的范围,通过解方程组求出交点的坐标,确定积分的上、下限.二、简单几何体的体积求抛物线 y2=2px(p>0)与直线 x=及 x 轴所围成的图形绕 x 轴旋转一周所得旋转体的体积.思路分析:先确定被积函数,再确定积分上、下限.求由曲线 y=与 y=x 所围成的图形绕 x 轴旋转一周所得旋转体的体积. 简单旋转体体积的求法与平面图形面积求法类似,只不过是被积函数由原来的 f(x)变成了 πf2(x).答案:活动与探究 1:解:如图,所求面积为:S=|sin x|dx=sin xdx-sin xdx=(-cos x)+cos =2+1=3.迁移与应用:解:如图,由得交点 A(-2,-4),B(1,-1).∴所围图形(阴影部分)的面积为S=(-x2-x+2)dx==.活动与探究 2:解:如图, y2=2px(p>0),∴f2(x)=2px,x∈,2∴V=πf2(x)dx=π2pxdx=πpx2=.迁移与应用:解:如图,由得 A(1,1),B(0,0).∴V=π(2x-x2)dx-πx2dx=π-π×x3=.1.曲线 y=cos x 与两坐标轴所围成的图形的面积为( ).A.4 B.2 C. D.32.若两曲线 y=x2与 y=cx3(c>0)围成的图形的面积为,则 c=( ).A. B. C.1 D.3.由曲线 y=,x+y=4 围成的平面图形绕 x 轴旋转而成的旋转体的体积为__________.4....