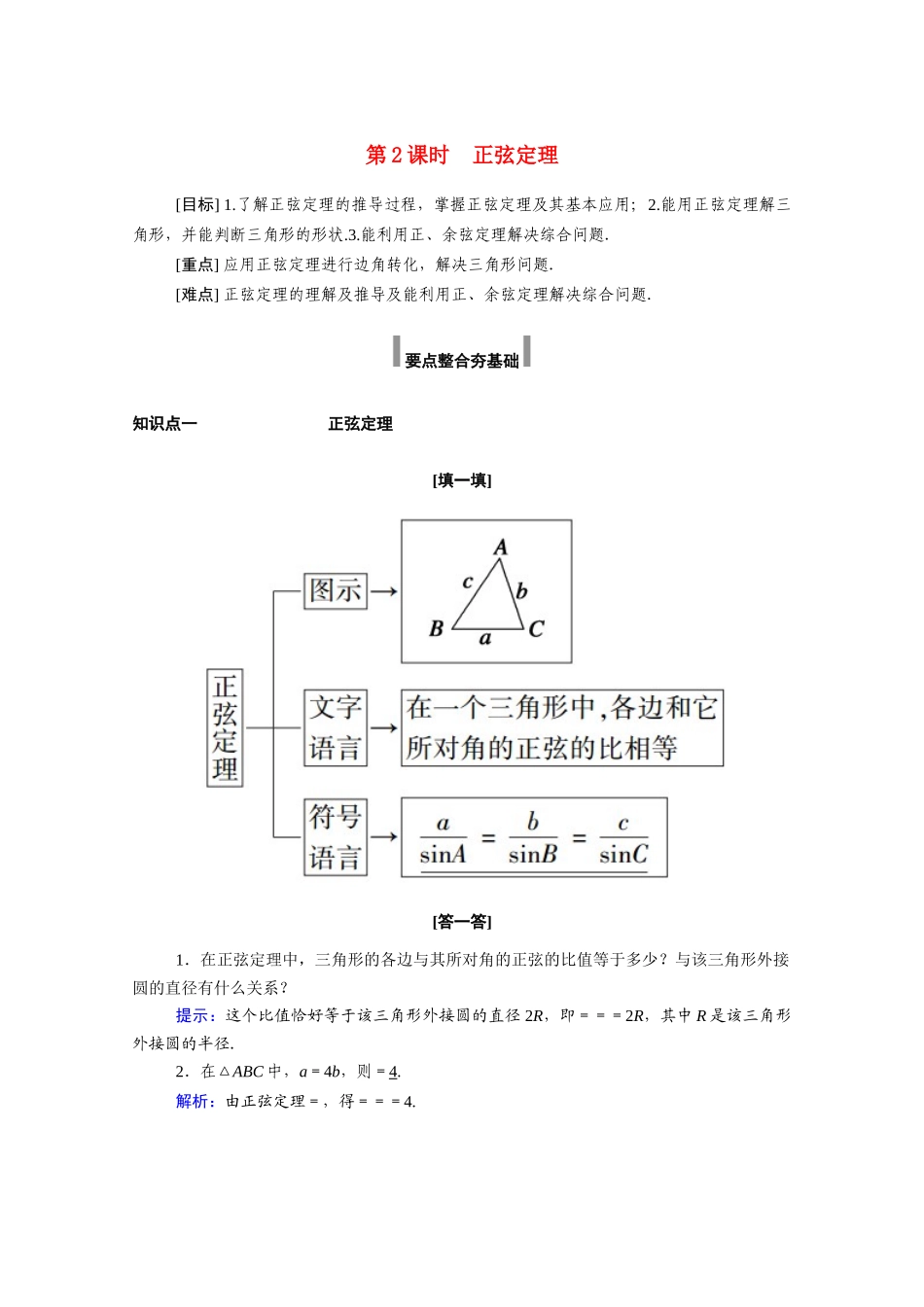
第 2 课时 正弦定理[目标] 1.了解正弦定理的推导过程,掌握正弦定理及其基本应用;2.能用正弦定理解三角形,并能判断三角形的形状.3.能利用正、余弦定理解决综合问题.[重点] 应用正弦定理进行边角转化,解决三角形问题.[难点] 正弦定理的理解及推导及能利用正、余弦定理解决综合问题. 要点整合夯基础 知识点一 正弦定理[填一填][答一答]1.在正弦定理中,三角形的各边与其所对角的正弦的比值等于多少?与该三角形外接圆的直径有什么关系?提示:这个比值恰好等于该三角形外接圆的直径 2R,即===2R,其中 R 是该三角形外接圆的半径.2.在△ABC 中,a=4b,则=4.解析:由正弦定理=,得===4.知识点二 正弦定理的变形公式[填一填]①a==,b==,c==;②a=2RsinA,b=2 R sin B ,c=2 R sin C ;③sinA=,sinB=,sinC=;④abc=sin A sin B sin C .其中,R 为△ABC 外接圆的半径.这些常见的公式的变形形式应熟练掌握,在解决具体问题时,根据不同的题设条件灵活选用不同的变形公式.[答一答]3.正弦定理的变形公式的作用是什么?正弦定理的适用范围是什么?提示:由正弦定理的变形公式可以实现三角形中边与角之间的相互转化,正弦定理对任意的三角形都成立.4.在△ABC 中,A>B 与 sinA>sinB 的关系怎样?提示:在△ABC 中,若 A>B,则 a>b.由正弦定理得 2RsinA>2RsinB,即 sinA>sinB.若 sinA>sinB,则 2RsinA>2RsinB(R 是△ABC 的外接圆半径).由正弦定理得 a>b.综上所述,在△ABC 中,A>B 与 sinA>sinB 等价.知识点三 利用正弦定理判断三角形的解的个数[填一填]已知三角形的两角和任意一边,求另两边和另一角,此时有唯一解,三角形被 唯一确定.已知两边和其中一边的对角,求其他的边和角,此时可能出现一解、两解或无解的情况,三角形不能被唯一确定.具体做法如下:由正弦定理得 sinB=,① 若>1,则满足条件的三角形个数为 0,即无解.② 若=1,则满足条件的三角形个数为 1,即一解.③ 若<1,则满足条件的三角形个数为 1 或 2 .[答一答]5.利用正弦定理能解什么条件下的三角形?提示:正弦定理的等式中有四个量,所以知其中三个,可求第四个.因此,知两角及一边可解三角形;知两边及一边的对角也可解三角形.6.在△ABC 中,已知 b=3,c=3,B=30°,判断三角形解的个数.提示:由正弦定理和已知条件,得 sinC==,∴C=60°或 C=120...