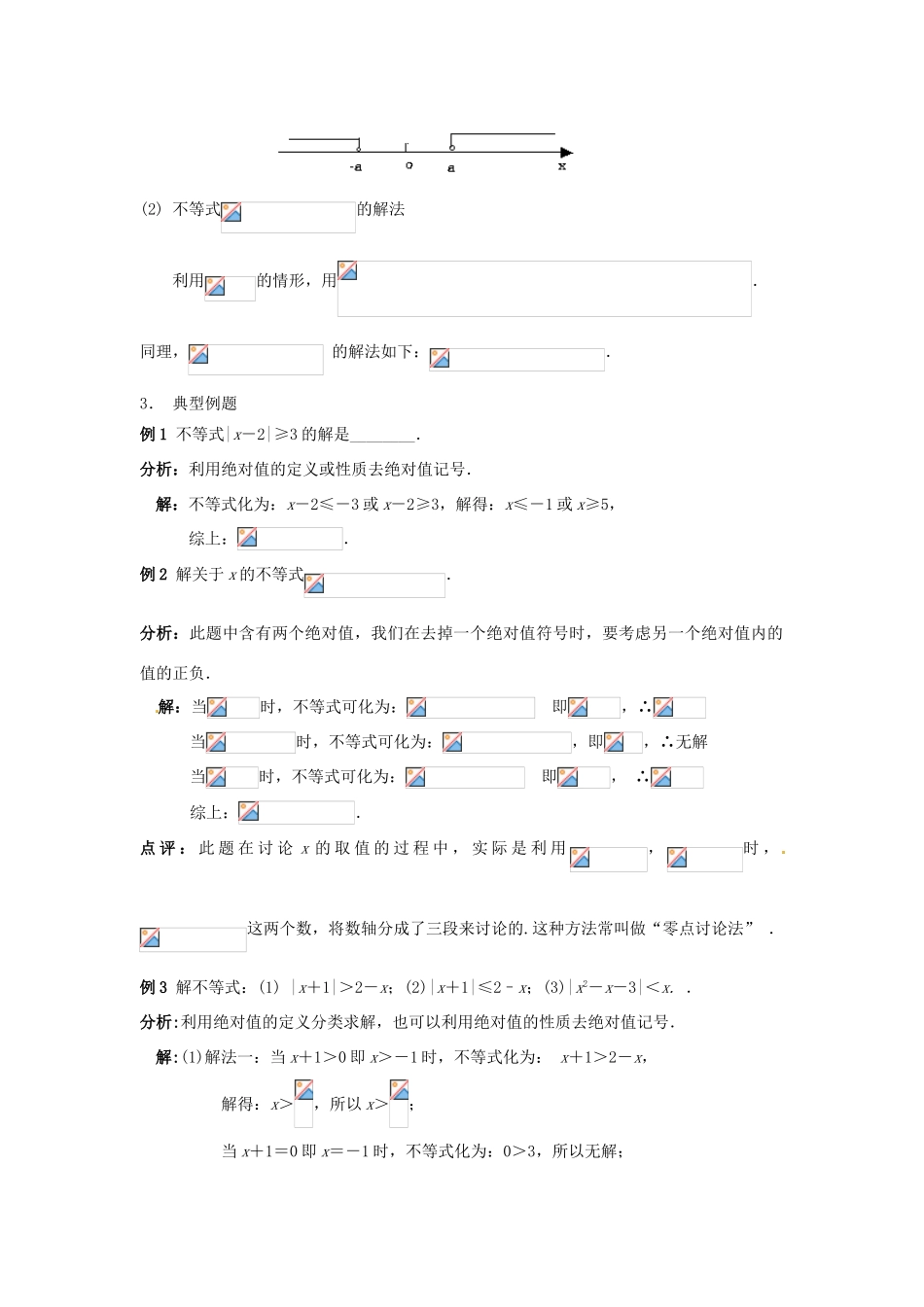
绝对值不等式一、 学习内容、要求及建议知识、方法要求建议解绝对值不等式定义理解解绝对值不等式的基本方法是将将原不等式转化为不含绝对值的不等式求解.去绝对值记号有多种方法,请根据题目适当选择性质几何意义图象二、 预习指导1. 预习目标(1) 回顾解绝对值的定义、绝对值的几何意义;(2) 解简单的绝对值不等式2. 预习提纲.(1) |x|<a (a>0) 的解法如何将不等式左边的绝对值符号去掉?——绝对值的意义.解法一:代数意义:|x|= 当时,不等式等价于 ,当时,不等式等价于 即,∴原不等式的解为.解法二:几何意义:|x|表示数轴上 x 的对应点 P 与原点 O 的距离|OP|.于是可以讨论 x 的符号,也可以运用其几何意义求解. 取 a =2, 则不等式|x|<2 的解集表示数轴上到原点 O 的距离小于 2 的所有点对应的实数 x. 于是不等式的解为.归纳:不等式|x|<a (a>0)的解为; 不等式|x|>a (a>0)的解集为. (2) 不等式的解法利用的情形,用.同理, 的解法如下:.3. 典型例题例 1 不等式|x-2|≥3 的解是________.分析:利用绝对值的定义或性质去绝对值记号.解:不等式化为:x-2≤-3 或 x-2≥3,解得:x≤-1 或 x≥5,综上:.例 2 解关于 x 的不等式.分析:此题中含有两个绝对值,我们在去掉一个绝对值符号时,要考虑另一个绝对值内的值的正负.解:当时,不等式可化为: 即,∴ 当时,不等式可化为:,即,∴无解 当时,不等式可化为: 即, ∴ 综上:.点 评 : 此 题 在 讨 论 x 的 取 值 的 过 程 中 , 实 际 是 利 用,时 ,这两个数,将数轴分成了三段来讨论的.这种方法常叫做“零点讨论法” .例 3 解不等式:(1) |x+1|>2-x;(2)|x+1|≤2–x;(3)|x2-x-3|<x. .分析:利用绝对值的定义分类求解,也可以利用绝对值的性质去绝对值记号.解:(1)解法一:当 x+1>0 即 x>-1 时,不等式化为: x+1>2-x,解得:x>,所以 x>;当 x+1=0 即 x=-1 时,不等式化为:0>3,所以无解;当 x+1<0 即 x<-1 时,不等式化为:-(x+1) >2-x,即-1>2,所以无解;综上所述,原不等式的解为 x>.解法二:原不等式化为:x+1>2-x 或 x+1<x-2,解得:x>,所以,原不等式的解为 x>.(2) 原不等式化为:x-2≤x+1≤2-x,解得:x,所以,原不等式的解为 x.(3) 不等式可化为:-x<x2-x-3<x,即∴原不...