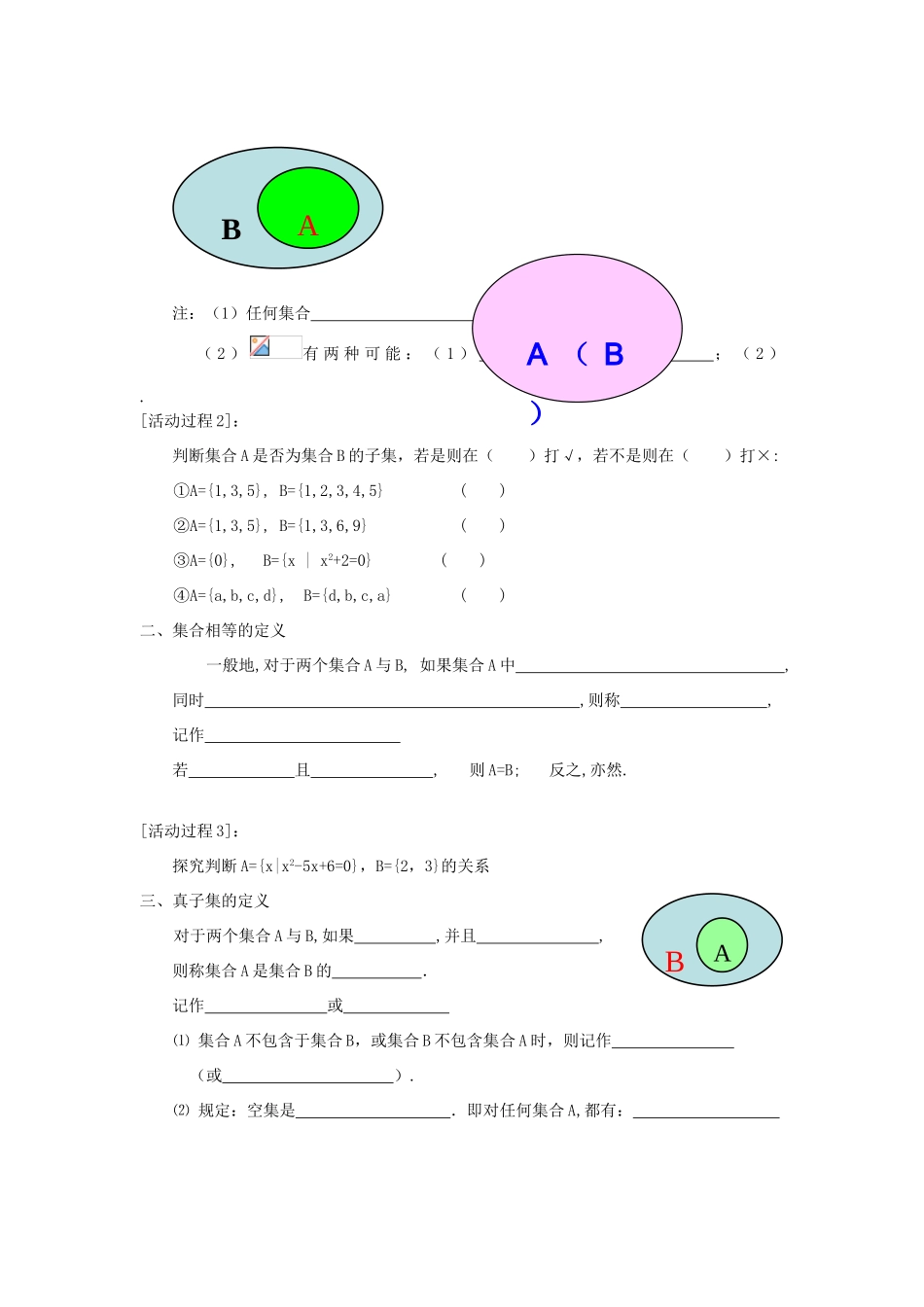
§1.2 集合的基本关系(学案)[学习目标]1、知识与技能 (1)理解子集、真子集概念. (2)会判断和证明两个集合包含关系. (3)理解“”、“”的含义. (4)会判断简单集合的相等关系.2、 过程与方法 (1)经历研究集合之间的关系的过程,学会探索研究问题的方法. (2)归纳整理本节所学知识.3、情感.态度与价值观 学习知道集合的基本关系,特别是相等关系为下一步学习运算作好准备,增强学习的积极性.[ 学习重点 ] : 子集的概念、真子集的概念.[ 学习难点 ] : 元素与子集、属于与包含间区别、描述法给定集合的运算.[学习方法]:合作式探究[ 学习用具 ] : 多媒体[ 学习过程 ] : 一、复习回顾集合的表示方法、集合的分类.【新课导入】 [活动过程 1]:观察以下几组集合,并指出它们元素间的关系:① A={偶数}, B=R;② A={x|x>0}, B={x|x>3};③ A={平行四边形}, B={正方形};④ A={x |x2+1=0}, B={x|x > 2} .二、讲授新课一、子集的概念一般地,对于两个集合 A 与 B,如果 我们就说 ,或 .记作 这时我们也说集合 A 是集合 B 的 注:(1)任何集合 ( 2 )有 两 种 可 能 : ( 1 ) ; ( 2 ) .[活动过程 2]:判断集合 A 是否为集合 B 的子集,若是则在( )打√,若不是则在( )打×:①A={1,3,5}, B={1,2,3,4,5} ( )②A={1,3,5}, B={1,3,6,9} ( )③A={0}, B={x | x2+2=0} ( )④A={a,b,c,d}, B={d,b,c,a} ( )二、集合相等的定义一般地,对于两个集合 A 与 B, 如果集合 A 中 ,同时 ,则称 ,记作 若 且 , 则 A=B; 反之,亦然.[活动过程 3]:探究判断 A={x|x2-5x+6=0},B={2,3}的关系三、真子集的定义对于两个集合 A 与 B,如果 ,并且 ,则称集合 A 是集合 B 的 .记作 或 ⑴ 集合 A 不包含于集合 B,或集合 B 不包含集合 A 时,则记作 (或 ).⑵ 规定:空集是 .即对任何集合 A,都有: BAA ( B)BA[例题讲解]例 1:某工厂生产的产品在质量和长度上都合格时,该产品才合格.若用 A 表示合格产品的集合,B 表示质量合格的产品的集合,C 表示长度合格的产品的集合,则下列包含关系哪些成立?A B, B A,A C, C A试用 Venn 图表示这三个集合的关系.例 2:写出{0,1,2}的所有子集,并指出其中哪些是它的真子集.例 3:设 A={x,x2,xy}, B={1,x,y},且 A=B,求实数 x,y 的值.例 4:若 A={x |-3≤x≤4}, B={x | 2m-1≤x≤m+1},当 B A 时,求实数 m 的取值范围. [课堂练习]1.教材 P9 . T 1,2,3,4,52.以下六个关系式:① φ{φ} φ∈{φ } ③ {0} φ ④0φ ⑤ φ≠{0} ⑥φ={φ},其中正确的序号是 [课堂小结]1. 2. 3. [作业布置]1.教材 P9 A 组 T2,3,52.已知 A={1,2,3,4}, B={x | x A}, 求 B.