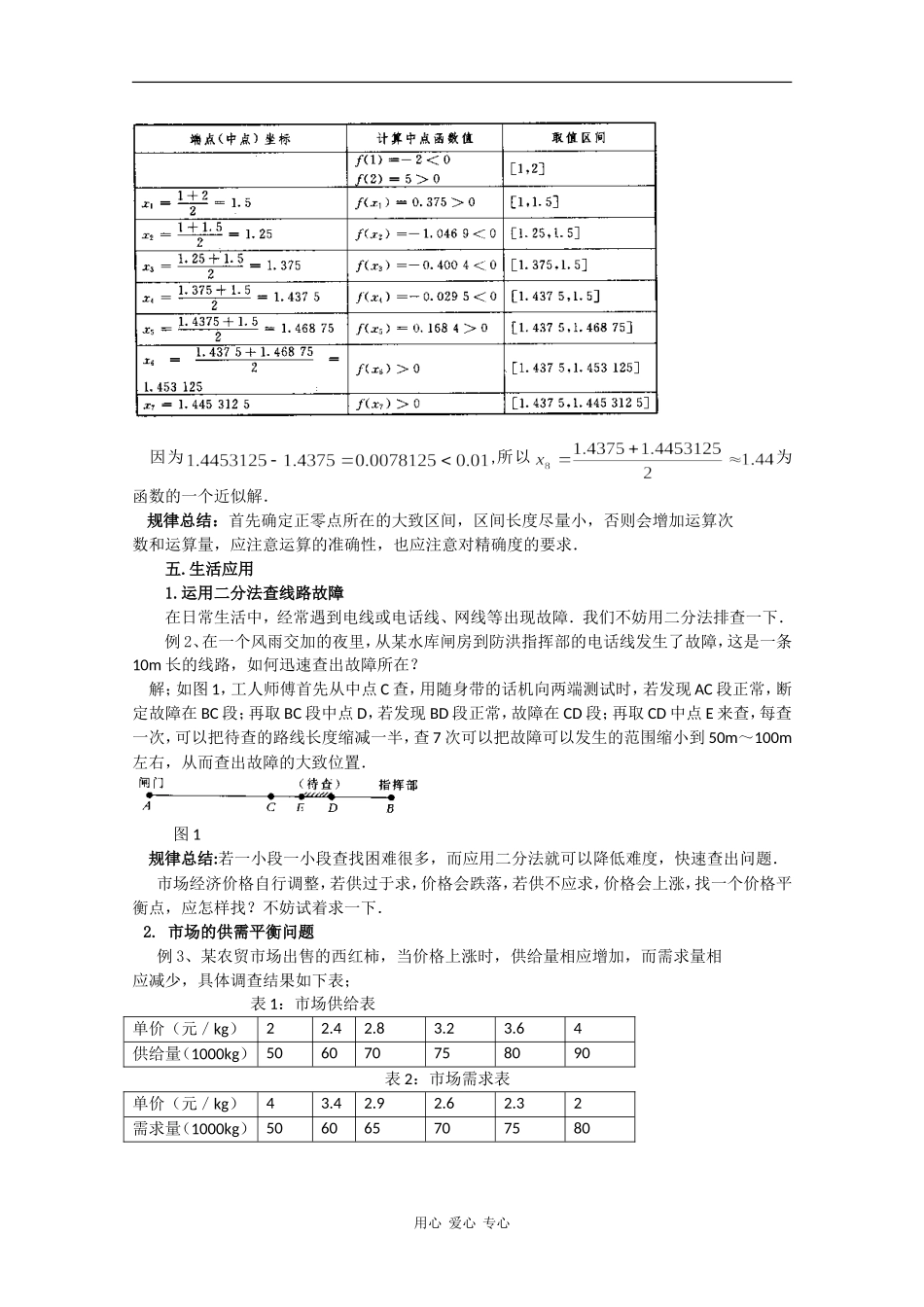
探究用二分法求方程的近似解的过程山东省利津县第一中学 胡彬 257400零点概念:对于函数 y=f(x),我们把使 f(x)=0 的实数 x 叫做函数 y=f(x)的零点. 方程f(x)=0 有实数根函数 y=f(x) 的图象与 x 轴有交点函数 y=f(x)有零点.如果函数 y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有 f(a).f(b)<0,那么,函数 y=f(x)在区间(a,b)内有零点,即存在 c(a,b),使得 f(c)=0,这个 c 也就是方程 f(x)=0的根. 一.为何要用二分法求方程的近似解 高次多项式方程公式解的探索史料:在十六世纪,已找到了三次和四次函数的求根公式,但对于高于 4 次的函数,类似的努力却一直没有成功,到了十九世纪,根据阿贝尔(Abel)和伽罗瓦(Galois)的研究,人们认识到高于 4 次的代数方程不存在求根公式,亦即不存在用四则运算及根号表示的一般的公式解.同时,即使对于 3 次和 4 次的代数方程,其公式解的表示也相当复杂,一般来讲并不适宜作具体计算.因此对于高次多项式函数及其它的一些函数,有必要寻求其零点的近似解的方法,这是一个在计算数学中十分重要的课题. 二.体会生活实例高沙至洞口的一条电话线路发生故障,请问如何去迅速查出故障之所在?解:如果沿着线路一小段一小段去查找,困难很多;每查一次要爬一次电杆,10KM 长的线路,大约有 200 多根电杆。维修人员这样工作最合理:①、先从中间位置板桥查起:若用随身所带的话机向两端测试,发现高沙到板桥段正常,则可确定板桥到洞口段有故障;②、再从中间位置花古处查,若板桥到花古段正常,则可确定故障出花古到洞口段。——————每查一次,则可将线路缩短一半,当把故障可能发生的范围缩小到 50m~100m 左右时,即只有一至两根电线杆时,则只要查几次就够了。————这种检查线路故障的方法,不仅可用于查找线路、水管、气管等故障,还能用于实验设计、资料查询等,同时也是我们所学的求方程的近似解的二分法方法。 三. 探究二分法的思想及步骤:1.出示例:有 12 个小球,质量均匀,只有一个是比别的球重的,你用天平称几次可以找出这个球的,要求次数越少越好. ( 让同学们自由发言,找出最好的办法)解:第一次,两端各放六个球,低的那一端一定有重球;第二次,两端各放三个球,低的那一端一定有重球;第三次,两端各放一个球,如果平衡,剩下的就是重球,否则,低的就是重球. 其实这就是一种二分法的思想,那什么叫二分法呢?2.定义二分法...