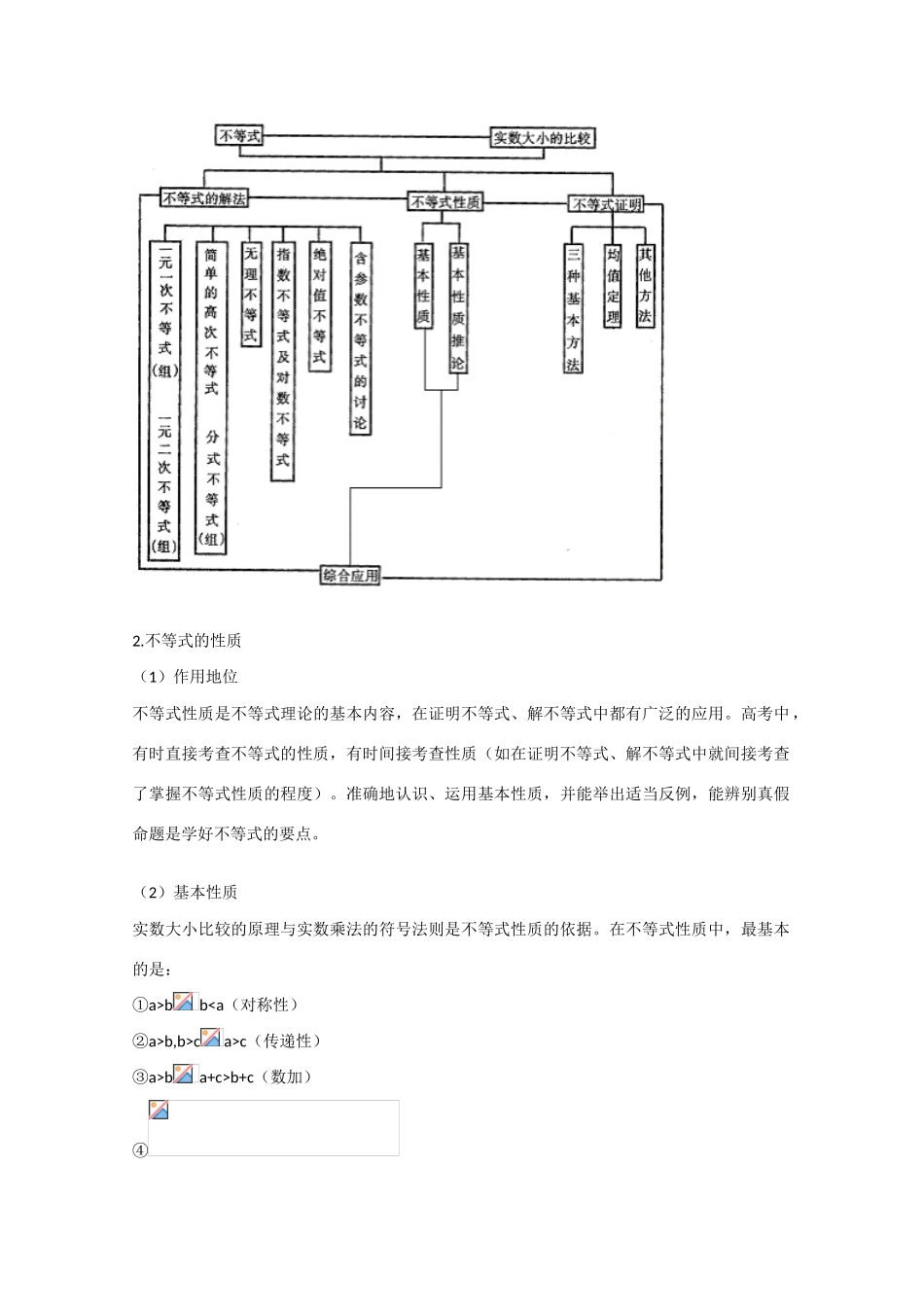
高考数学知识模块复习指导系列学案——不等式【I】【考点梳理】一、考试内容不等式,不等式的性质,不等式的证明,不等式的解法,含有绝对值的不等式。二、考试要求1.掌握不等式的性质及其证明,掌握证明不等式的几种常用方法,掌握两个和三个(不要求四个和四个以上)“正数的算术平均数不小于它们的几何平均数”这两个定理,并能运用上述性质、定理和方法解决一些问题。2.在熟练掌握一元一次不等式(组)、一元二次不等式(组)的解法的基础上初步掌握其他的一些简单的不等式的解法。3.会用不等式||a|-|b||≤|a+b|≤|a|+|b|。三、考点简析1.不等式知识相互关系表2.不等式的性质(1)作用地位不等式性质是不等式理论的基本内容,在证明不等式、解不等式中都有广泛的应用。高考中,有时直接考查不等式的性质,有时间接考查性质(如在证明不等式、解不等式中就间接考查了掌握不等式性质的程度)。准确地认识、运用基本性质,并能举出适当反例,能辨别真假命题是学好不等式的要点。(2)基本性质实数大小比较的原理与实数乘法的符号法则是不等式性质的依据。在不等式性质中,最基本的是:①a>bb
b,b>ca>c(传递性)③a>ba+c>b+c(数加)④(a>b,c=0a·c=b·c)与等式相比,主要区别在数乘这一性质上,对于等式 a=bac=bc,不论 c 是正数、负数还是零,都成立,而对于不等式 a>b,两边同乘以 c 之后,ac 与 bc 的大小关系就需对 c 加以讨论确定。这关系即使记得很清楚,但在解题时最容易犯的毛病就是错用这一性质,尤其是需讨论参数时。(3)基本性质的推论由基本性质可得出如下推论:推论 1:a>b>0,c>d>0ac>bd推论 2:a>b>0,c>d>0推论 3:a>b>0an>bn(n∈N)推论 4:a>b>0(n∈N)对于上述推论可记住两点:一是以上推论中 a,b,c,d 均为正数,即在{x|x 是正实数}中对不等式实施运算;二是直接由实数比较大小的原理出发。3.不等式的证明(1)作用地位证明不等式是数学的重要课题,也是分析、解决其他数学问题的基础,特别是在微积分中,不等式是建立极限论的理论基础。高考中,主要涉及“a,b>0 时,a+b≥2”这类不等式,以及运用不等式性质所能完成的简单的不等式的证明。用数学归纳法证明的与自然数有关命题的不等式难度较大。(2)基本不等式定理 1:如果 a,b∈{x|x 是正实数},那么≥(当且仅当 a=b 时取“=”号)定理 2:如果 a,b,c∈{x|x 是正实数},那么≥(当且仅当 a=b=c 时取“=”号)定理 3:如果 a...