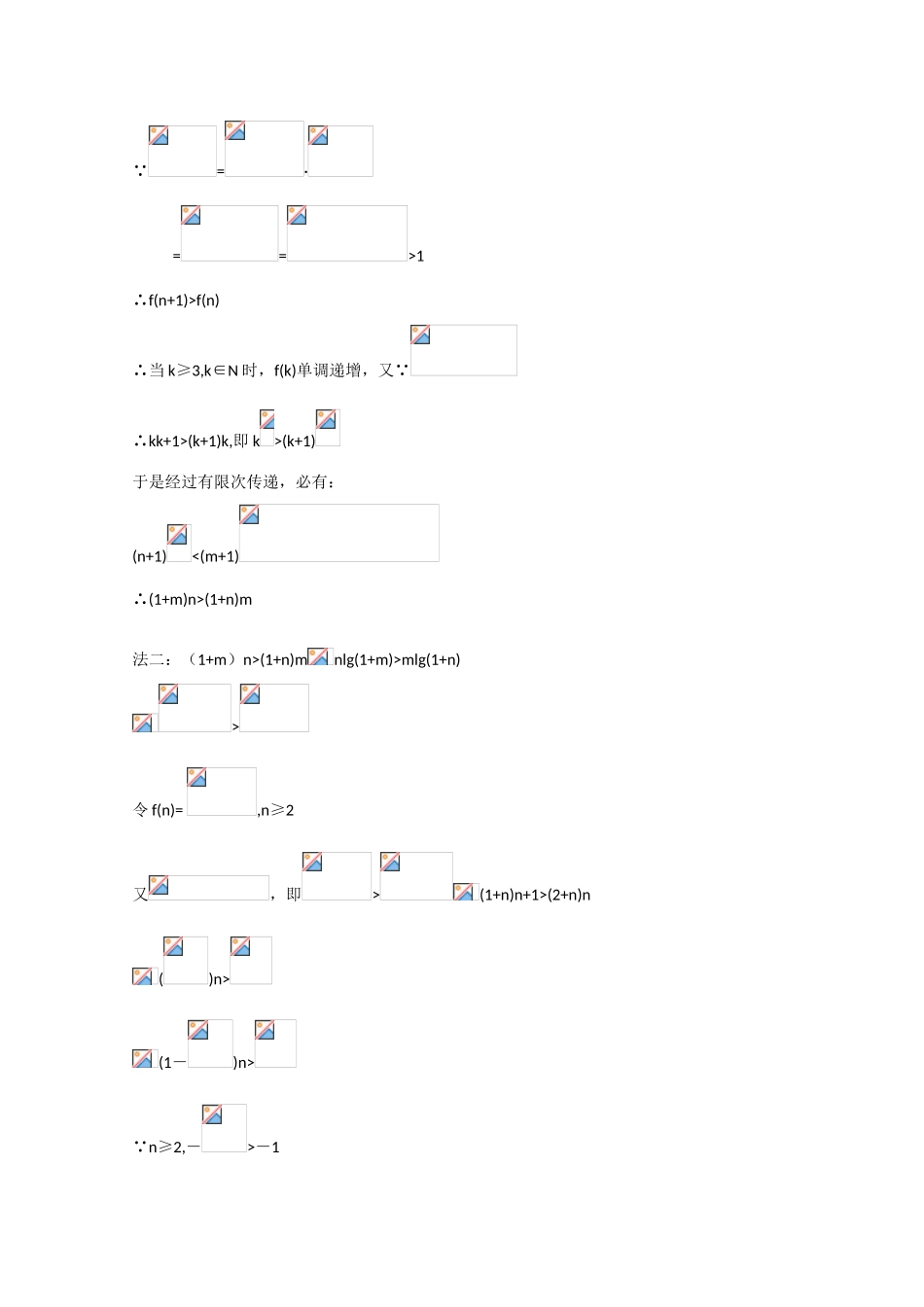
高考数学知识模块复习指导系列学案——不等式【II】例 3 已知 i、m、n 是正整数,且 1,所以>即 miAni>niAmi(2)由二项式定理有(1+m)n=1+Cn1m+Cn2m2+…+Cnnmn(1+n)m=1+Cm1n+Cm2n2+…+Cmmnm由(1)知 miAni>niAmi (1niCmi (ki≤m,…mmCnm> nmCmm, mm+1Cnm+1 >0,…, mmCnn >0,∴1+ Cn1m + Cn2m2+…+ Cnnmn >1+ Cm1n+ Cm2n2 +…+ Cmmnn,即(1+m)n>(1+n)m 成立。注 本题是 2001 年全国高考数学试题,上述证明方法关键是配对。除了上述证法外,本题还有许多另外的证法,下面另举两种证法。(1)法一:令 n=m+k,(k∈N)对自然数 t=1,2,…,i-1,tm·(m+k) ∴m(m+k) 21∴f(n+1)>f(n)∴当 k≥3,k∈N 时,f(k)单调递增,又 ∴kk+1>(k+1)k,即 k>(k+1)于是经过有限次传递,必有:(n+1)<(m+1)∴(1+m)n>(1+n)m法二:(1+m)n>(1+n)mnlg(1+m)>mlg(1+n)>令 f(n)= ,n≥2又,即>(1+n)n+1>(2+n)n()n>(1-)n> n≥2,->-1∴由贝努利不等式得(1-)n>1-=>∴>,∴f(n)单调递减,又 m∴(1+m)n>例 4 解下列关于 x 的不等式:(1)a2x+1≤ax+2+ax-2(a>0);(2)loga(1-)>1(a>0 且 a≠1)。解在解指、对数不等式时,常要对底数 a 进行分类,然后依据其函数的单调性来实现转化,在转化过程中注意不等式解的等价性。(1)原不等式等价于a2x...