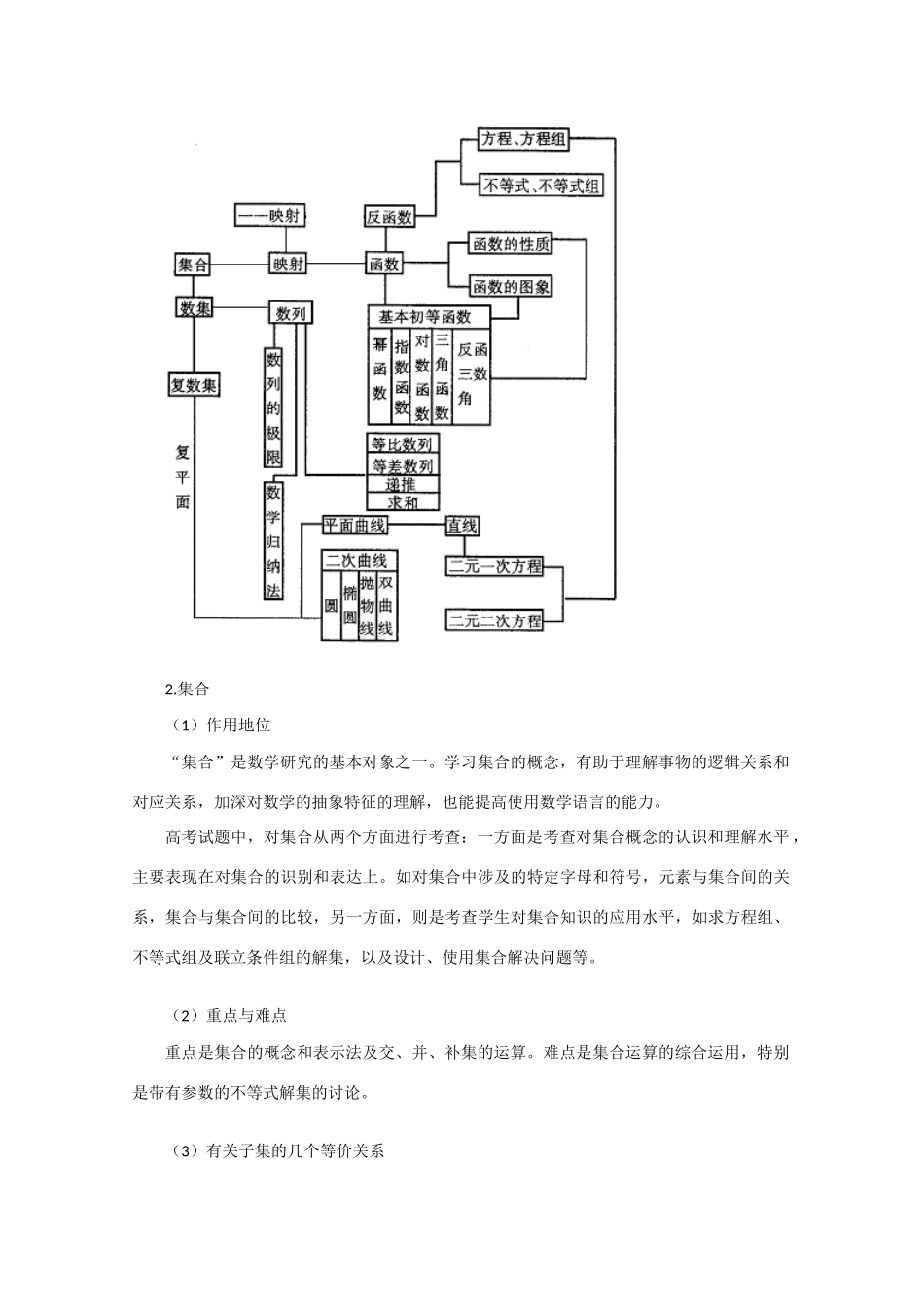
考点梳理一、考试内容集合、子集、交集、并集、补集。|ax+b|c(c>0)型不等式。一元二次不等式。映射、函数。分数指数幂与根式。函数的单调性,函数的奇偶性。反函数,互为反函数的函数图像间的关系。指数函数。对数,对数的性质和运算法则。对数函数,换底公式。简单的指数方程和对数方程。二、考试要求1.理解集合、子集、交集、并集、补集的概念。了解空集和全集的意义。了解属于、包含、相等关系的意义。能掌握有关的术语和符号,能正确地表示一些较简单的集合。2.理解|ax+b|c(c>0)型不等式的概念,并掌握它们的解法。了解二次函数、一元二次不等式及一元二次方程三者之间的关系,掌握一元二次不等式的解法。3.了解映射的概念,在此基础上理解函数及其有关的概念,掌握互为反函数的函数图像间的关系。4.理解函数的单调性和奇偶性的概念,并能判断一些简单函数的单调性和奇偶性。能利用函数的奇偶性来描绘函数的图像。5.理解分数指数幂、根式的概念,掌握分数指数幂的运算法则。6.理解对数的概念,掌握对数的性质。7.掌握指数函数、对数函数的概念及其图像和性质,并会解简单的指数方程和对数方程。三、考点简析1.函数及相关知识关系表2.集合(1)作用地位“集合”是数学研究的基本对象之一。学习集合的概念,有助于理解事物的逻辑关系和对应关系,加深对数学的抽象特征的理解,也能提高使用数学语言的能力。高考试题中,对集合从两个方面进行考查:一方面是考查对集合概念的认识和理解水平 ,主要表现在对集合的识别和表达上。如对集合中涉及的特定字母和符号,元素与集合间的关系,集合与集合间的比较,另一方面,则是考查学生对集合知识的应用水平,如求方程组、不等式组及联立条件组的解集,以及设计、使用集合解决问题等。(2)重点与难点重点是集合的概念和表示法及交、并、补集的运算。难点是集合运算的综合运用,特别是带有参数的不等式解集的讨论。(3)有关子集的几个等价关系①A∩B=AAB;②A∪B=BAB;③ABC uAC uB;④A∩CuB =CuAB;⑤CuA∪B=IAB。(4)交、并集运算的性质①A∩A=A,A∩=,A∩B=B∩A;②A∪A=A,A∪=A,A∪B=B∪A;③Cu (A∪B)= CuA∩CuB,Cu (A∩B)= CuA∪CuB;(5)有限子集的个数:设集合 A 的元素个数是 n,则 A 有 2n个子集,2n-1 个非空子集。3.函数的性质(1)函数的概念:定义域、值域、对应法则、反函数、复合函数、分段函数;(2)函数的性质:单调性、奇偶性、有界性...