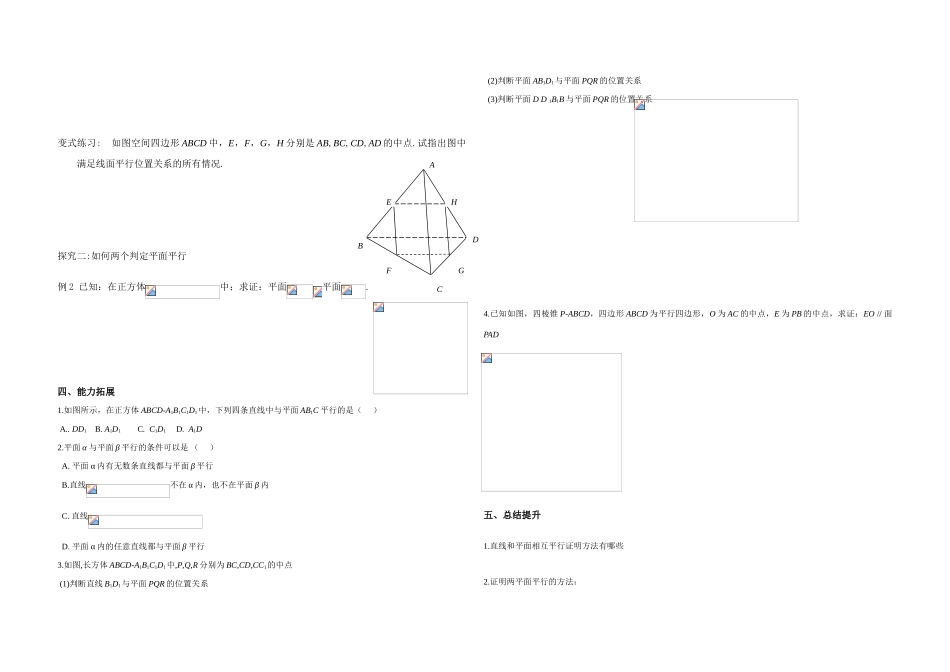
平行关系的判定 (学案)一、学习目标1.理解并掌握线面平行与两个平面平行的定义.2.掌握线面平行与两个平面平行的判定定理的证明.3.会画平行或相交平面的空间图形,并用字母或符号表示,进一步培养学生的空间想象能力.二、学习重点、难点1.学习重点:掌握线面平行与两个平面平行的判定定理.2.学习难点:掌握平行的判定定理的证明及其应用.学习过程:一、课前准备:阅读课本 P 2 8 – 3 1 自主学习1.直线和平面的位置关系有 、 、 2.两个平面的位置关系有 、 3.直线与面平行的判定 4.平面与面平行的判定 自主测评1.下列条件中,能得出直线 a 与平面 α 平行的条件是( )2.判断下列命题的正误.(1).如果一个平面内的所有直线都和另一个平面平行,那么这两个平面平行.(2). 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(3).垂直于同一直线的两直线平行.(4).分别在两个平行平面内的两条直线都平行(5).如果一个平面内的无数条直线平行于另一个平面,那么这两个平面平行.(6).如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行.(7).如果一条直线平行于平面内的无数条直线,则此直线行平该平面.二、新课导学探究一:如何两个判定直线与平面平行三、巩固应用例 1.已知:空间四边形 ABCD 中,E、F 分别是 AB、AD 的中点. 判断 EF 与平面 BCD 的位置关系.EFABDαC变式练习: 如图空间四边形 ABCD 中,E,F,G,H 分别是 AB,BC,CD,AD 的中点.试指出图中满足线面平行位置关系的所有情况.探究二:如何两个判定平面平行例 2 已知:在正方体中;求证:平面平面.四、能力拓展1.如图所示,在正方体 ABCD-A1B1C1D1中,下列四条直线中与平面 AB1C 平行的是( ) A.. DD1 B. A1D1 C. C1D1 D. A1D 2.平面 α 与平面 β 平行的条件可以是 ( )A. 平面 α 内有无数条直线都与平面 β 平行B.直线不在 α 内,也不在平面 β 内C. 直线D. 平面 α 内的任意直线都与平面 β 平行3.如图,长方体 ABCD-A1B1C1D1中,P,Q,R 分别为 BC,CD,CC1的中点 (1)判断直线 B1D1与平面 PQR 的位置关系(2)判断平面 AB1D1与平面 PQR 的位置关系(3)判断平面 D D 1B1B 与平面 PQR 的位置关系 4.已知如图,四棱锥 P-ABCD,四边形 ABCD 为平行四边形,O 为 AC 的中点,E 为 PB 的中点,求证:EO // 面PAD五、总结提升1.直线和平面相互平行证明方法有哪些2.证明两平面平行的方法:BCEHADFG(1)利用定义证明 (2)判定定理 (3)垂直于同一直线的两个平面平行.用符号表示是:a⊥α,a⊥β 则 α∥β. (4)平行于同一个平面的两个平面平行.