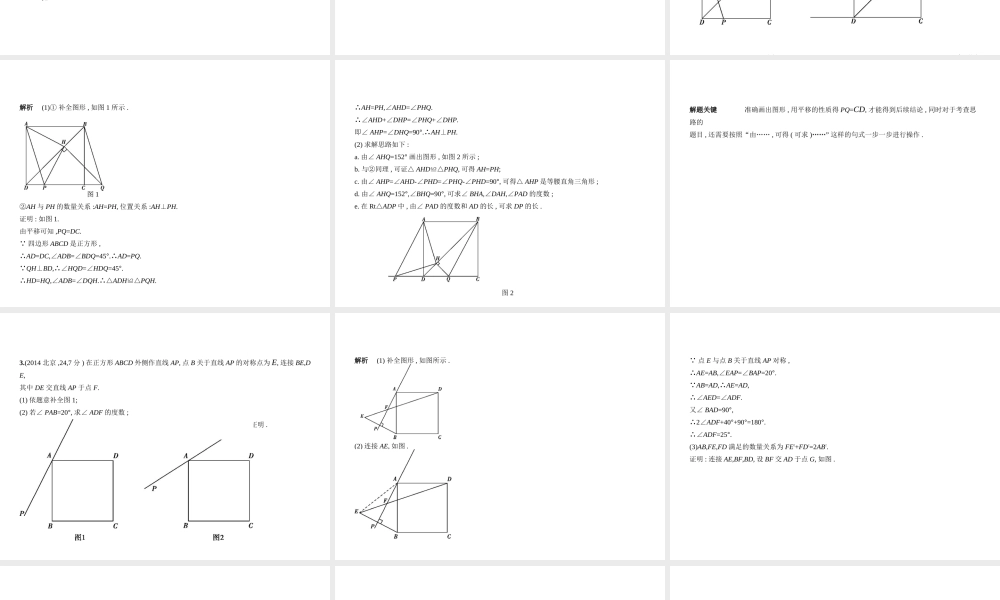
§7.6 几何压轴综合题中考数学 ( 北京专用 )1.(2018 北京 ,27,7 分 ) 如图 , 在正方形 ABCD 中 ,E 是边 AB 上的一动点 ( 不与点 A,B 重合 ), 连接 DE, 点A 关于直线 DE 的对称点为 F, 连接 EF 并延长交 BC 于点 G, 连接 DG, 过点 E 作 EH⊥DE 交 DG 的延长线于点 H, 连接 BH.(1) 求证 :GF=GC;(2) 用等式表示线段 BH 与 AE 的数量关系 , 并证明 . 好题精练解析 (1) 证明 : 如图 , 连接 DF. 四边形 ABCD 为正方形 ,∴DA=DC=AB,∠A=∠C=∠ADC=90°.又 点 A 关于直线 DE 的对称点为 F,∴△ADE≌△FDE,∴DA=DF=DC,∠DFE=∠A=90°,∴∠DFG=90°.在 Rt△DFG 和 Rt△DCG 中 , ∴Rt△DFGRt≌△DCG(HL),,,DGDGDFDC∴GF=GC.(2) 线段 BH 与 AE 的数量关系 :BH= AE.证明 : 在线段 AD 上截取 AM, 使 AM=AE, 连接 ME. AD=AB,∴DM=BE.由 (1) 得∠ 1=2,3=4,∠ ∠∠ ∠ADC=90°,∴∠1+2+3+4=90∠∠∠°,∴22+23=90∠∠°,∴∠2+3=45∠°,2∴∠EDH=45°. EH⊥DE,∴DE=EH, ∠DEH=90°,∠A=90°,∴∠1+∠AED=90°,5+∠∠AED=90°,∴∠1=5.∠在△ DME 和△ EBH 中 , ∴△DME≌△EBH(SAS),∴ME=BH. ∠A=90°,AM=AE,∴ME= AE,∴BH= AE.,15,,DMEBDEEH 22思路分析 本题第 (1) 问需要通过正方形的性质和轴对称的性质解决 ; 本题第 (2) 问需要通过构造全等三角形 , 利用等腰直角三角形的性质解决 .解题关键 解决本题第 (2) 问的关键是要通过截取得到等腰直角三角形 , 并借助 SAS 证明三角形全等 , 从而将 BH 和 AE 转化到△ AME 中证明数量关系 .2.(2015 北京 ,28,7 分 ) 在正方形 ABCD 中 ,BD 是一条对角线 . 点 P 在射线 CD 上 ( 与点 C,D 不重合), 连接 AP, 平移△ ADP, 使点 D 移动到点 C, 得到△ BCQ, 过点 Q 作 QH⊥BD 于点 H, 连接 AH,PH.(1) 若点 P 在线段 CD 上 , 如图 1.① 依题意补全图 1;② 判断 AH 与 PH 的数量关系与位置关系并加以证明 ;(2) 若点 P 在线段 CD 的延长线上 , 且∠ AHQ=152°, 正方形 ABCD 的边长为 1, 请写出求 DP 长的思路 .( 可以不写出计算结果 ) 图 1 备用图解析 (1)① 补全图形 , 如图 1 所示 . 图 1②AH 与 PH 的数量关系 :AH=PH, 位置关系 :AH⊥PH.证明...