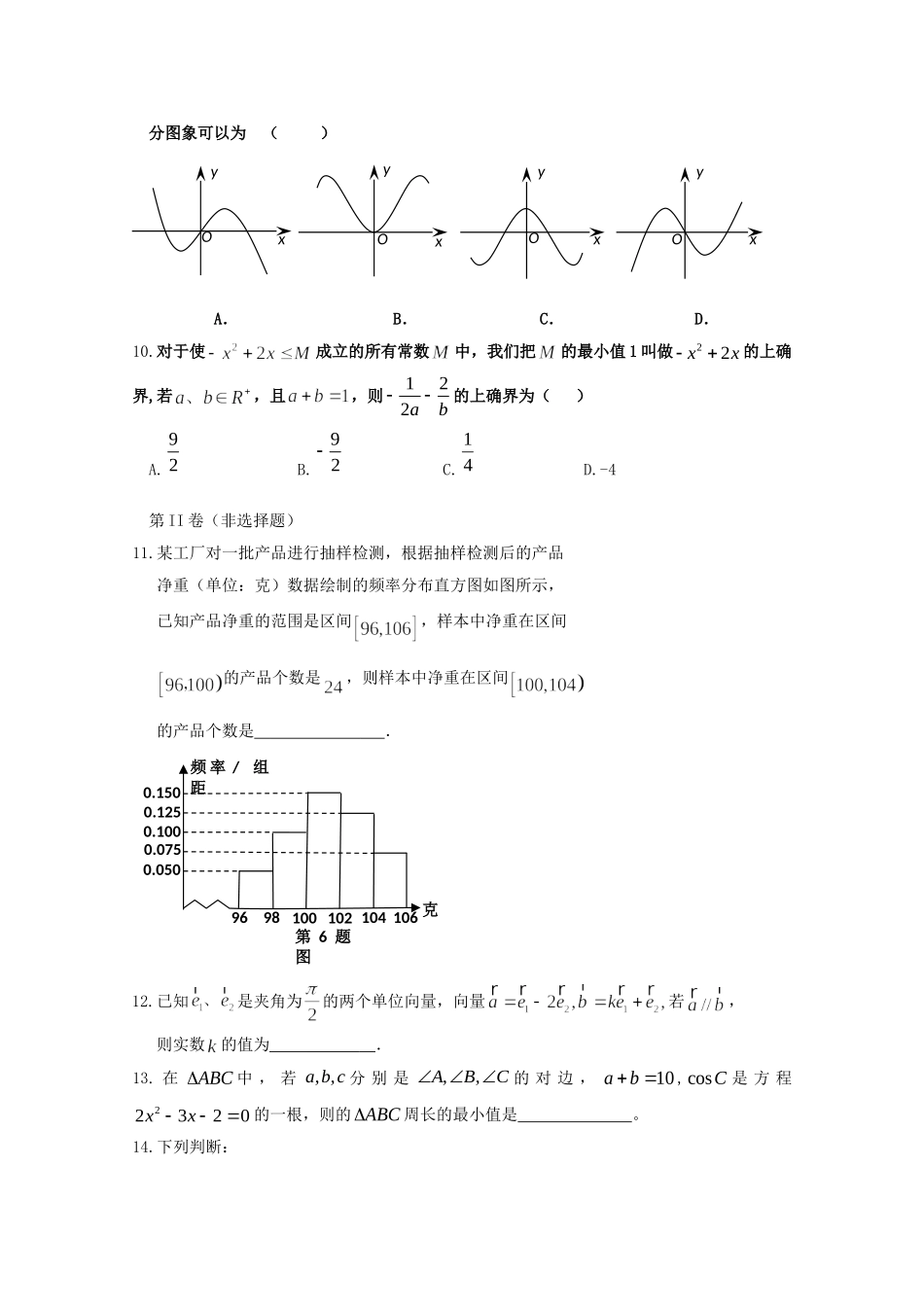
本套试卷的知识点:集合与简易逻辑基本初等函数数列三角函数平面向量不等式空间几何体圆锥曲线与方程导数及其应用概率统计第I卷(选择题)1.(2016新课标高考题)已知等差数列前9项的和为27,,则(A)100(B)99(C)98(D)972.由“若ab,则acbc”推理到“若ab,则acbc”是()A.归纳推理B.类比推理C.演绎推理D.不是推理3.曲线1yxx=-上一点7(4,)4P-处的切线方程是()A.51680xy+-=B.51680xy-+=C.51680xy++=D.51680xy--=4.已知某离散型随机变量服从的分布列如,则随机变量的方差等于()A.B.C.D.5.已知函数则=.1..0.6.若,则()A.0B.1C.2D.37.二项式展开式中的系数为()(A).(B).(C).(D).8.设满足约束条件,则的取值范围是()A.B.C.D.9.设曲线在其上任一点处的切线的斜率为,则函数的部分图象可以为()A.B.C.D.10.对于使成立的所有常数中,我们把的最小值1叫做22xx的上确界,若,且,则122ab的上确界为()A.92B.92C.41D.-4第II卷(非选择题)11.某工厂对一批产品进行抽样检测,根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图如图所示,已知产品净重的范围是区间,样本中净重在区间的产品个数是,则样本中净重在区间的产品个数是.12.已知是夹角为的两个单位向量,向量若,则实数的值为.13.在ABC中,若,,abc分别是,,ABC的对边,10ab,cosC是方程22320xx的一根,则的ABC周长的最小值是。14.下列判断:OxxxxyyyyOOO第6题图克频率/组距0.1500.1250.1000.0750.0509698100102104106(1)命题“若q则p”与“若p则q”互为逆否命题;(2)“22ambm”是“ab”的充要条件;(3)“矩形的两条对角线相等”的否命题是假命题;(4)命题“1,2”为真命题,其中正确的序号是。15.如图,在直三棱柱中,,,,点分别在棱上,且.(1)求四棱锥的体积;(2)求所在半平面与所在半平面所成二面角的余弦值.16.已知椭圆的中心在坐标原点,焦点在坐标轴上,且经过两点,是上的动点.(1)求的最大值;(2)若平行于的直线在轴上的截距为,直线交椭圆于两个不同点,求证:直线与直线的倾斜角互补.17.已知.(1)当时,判断的奇偶性,并说明理由;(2)当时,若,求的值;(3)若,且对任何不等式恒成立,求实数的取值范围.ABCEC1A1B1F【KS5U】2015-2016下学期高二数学暑假作业三试卷答案1.【答案】C【解析】试题分析:由已知,所以故选C.考点:等差数列及其运算2.B3.C4.B5.B6.C7.D8.D9.A10.B11.4412.13.105314.(1)(3)(4)15.(1)……7分(2)建立如图所示的直角坐标系,则,,,,,……………………2分设平面的法向量为,则,所以……………………………2分平面的法向量为,则所以所在半平面与所在半平面所成二面角的余弦值为.16.(1)设椭圆的方程为将代入椭圆的方程,得………2分解得,所以椭圆E的方程为…………2分设点的坐标为,则.又是上的动点,所以,得,代入上式得,故时,.的最大值为.………………2分(2)因为直线平行于,且在轴上的截距为,又,所以直线的方程为.由得………………2分设、,则.又故.………2分又,所以上式分子………2分故.所以直线与直线的倾斜角互补.…………………………………2分17.(1)当时,既不是奇函数也不是偶函数.……2分∵,∴所以既不是奇函数,也不是偶函数.………………………………………2分(2)当时,,由得……………………………2分即或………………………2分解得所以或.………………2分(3)当时,取任意实数,不等式恒成立,故只需考虑,此时原不等式变为即………………………………………………………2分故又函数在上单调递增,所以;对于函数①当时,在上单调递减,,又,所以,此时的取值范围是.……………………………………2分②当,在上,,当时,,此时要使存在,必须有即,此时的取值范围是综上,当时,的取值范围是;当时,的取值范围是;当时,的取值范围是.