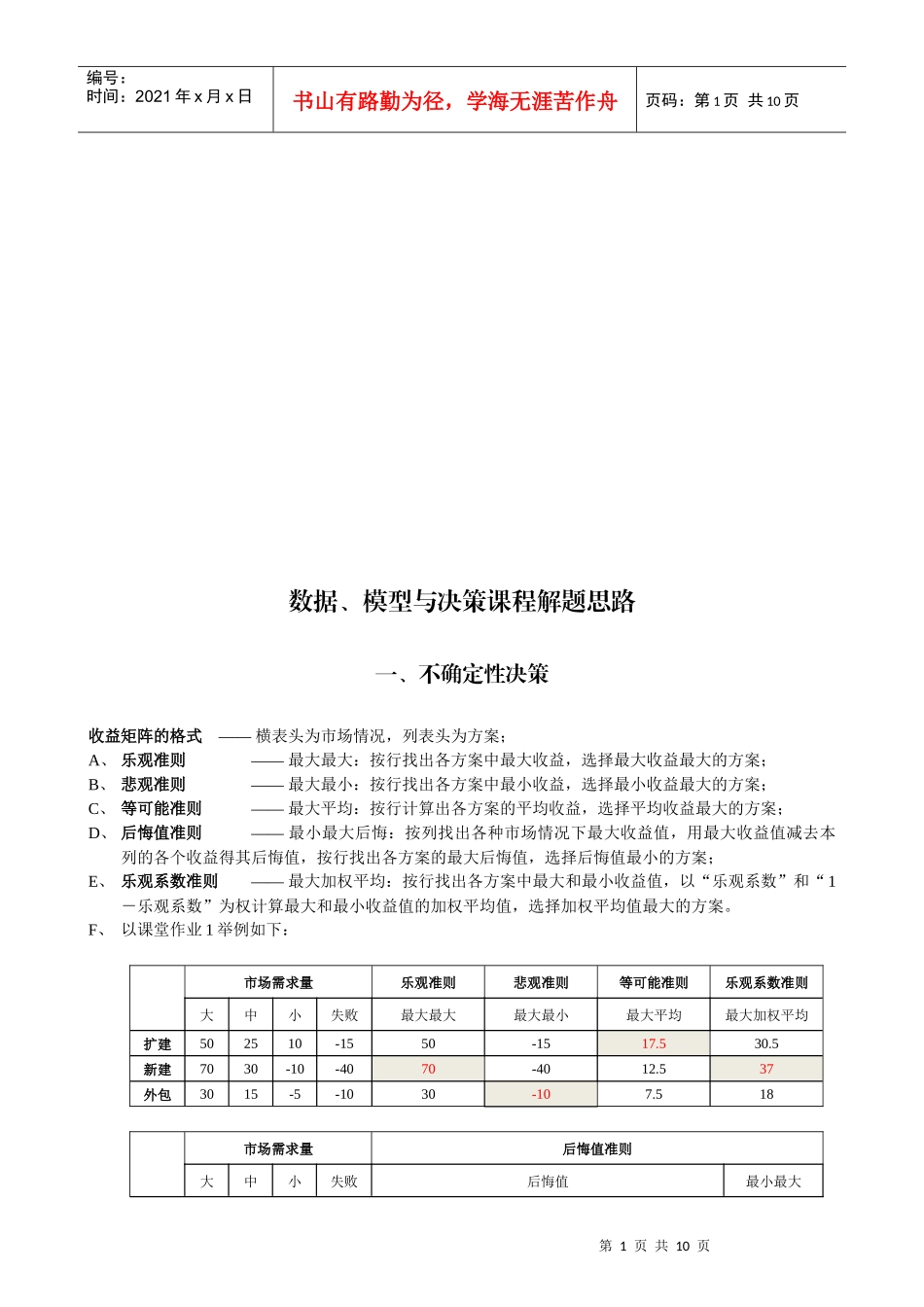
第1页共10页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第1页共10页数据、模型与决策课程解题思路一、不确定性决策收益矩阵的格式——横表头为市场情况,列表头为方案;A、乐观准则——最大最大:按行找出各方案中最大收益,选择最大收益最大的方案;B、悲观准则——最大最小:按行找出各方案中最小收益,选择最小收益最大的方案;C、等可能准则——最大平均:按行计算出各方案的平均收益,选择平均收益最大的方案;D、后悔值准则——最小最大后悔:按列找出各种市场情况下最大收益值,用最大收益值减去本列的各个收益得其后悔值,按行找出各方案的最大后悔值,选择后悔值最小的方案;E、乐观系数准则——最大加权平均:按行找出各方案中最大和最小收益值,以“乐观系数”和“1-乐观系数”为权计算最大和最小收益值的加权平均值,选择加权平均值最大的方案。F、以课堂作业1举例如下:市场需求量乐观准则悲观准则等可能准则乐观系数准则大中小失败最大最大最大最小最大平均最大加权平均扩建502510-1550-1517.530.5新建7030-10-4070-4012.537外包3015-5-1030-107.518市场需求量后悔值准则大中小失败后悔值最小最大第2页共10页第1页共10页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第2页共10页扩建502510-152050520新建7030-10-4000203030外包3015-5-10401515040二、规划模型的标准化解题思路:标准形式的约束条件有三个要件,一是常数项非负;二是只能有等式;三是定义域非负。根据上述要件,分四步操作:A、判断常数项是否非负,如有负值则两边同乘(-1),并相应改变不等号方向;B、判断是否有不等式,如有则设松弛或剩余变量xi≥0,大于号减、小于号加xi变等式;C、判断各变量的定义域是否非负,如为负值,则设xj=(-xi)≥0,代入模型;如为-∞≤xk≤∞,则设xk=(xm-xn),xm、xn≥0,代入模型;D、整理变量下标后,得到标准形式。三、线性规划模型的解法及敏感性分析A、图解步骤如下:1、以x1为横轴、x2为纵轴建立直角坐标系,标出各约束条件和目标函数的直线;2、在第一象限找出可行域;3、目测目标函数平移后最可能与可行域的哪个顶点相切,则该点为最优解点;4、解方程得到该点坐标,即得最优解,代入目标函数得最优值。5、小技巧:(1)作图时,对约束条件,可分别令x1和x2为零,得到其与纵轴和横轴的交点,连接即可;对目标函数,令x1为一特殊值,得出x2,再与原点相连,可得函数直线,再沿横轴平移到合适位置即;(2)各条直线斜率绝对值越大的,越接近垂直于x1轴;(3)确定可行域时,要考虑坐标轴和原点;(4)目测判断最优点不易时,可将相邻数点的坐标解出代入目标函数进行比较。B、松弛变量和剩余变量1、约束条件为“≤”的存在松弛变量,为“≥”的存在剩余变量;2、将最优解代入各约束条件即得各自的松弛或剩余变量;3、构成最优解的约束条件的松弛或剩余变量为零。C、对偶价格1、不构成最优解的约束条件的对偶价格为零;2、构成最优解的约束条件存在对偶价格,求解时令其中一个约束条件的常数项增加1,另一个约束条件不变,重新解出交点坐标,代回目标函数计算目标值,再与原最优值相差即得;第3页共10页第2页共10页编号:时间:2021年x月x日书山有路勤为径,学海无涯苦作舟页码:第3页共10页3、对偶价格的讨论均在各约束条件常数项的上、下限范围内进行,超范围时对偶价格可能发生变化;4、已知对偶价格和最优值求常数项变化时,目标函数求Max时,增加目标值的,常数项同向变化,即增大;求Min时,增加目标值的,常数项反向变化,即减少;反之亦然。D、目标函数系数上、下限1、目标函数系数的变化,在图解时可视为目标函数直线斜率的变动,即该直线以最优解点为支点旋转;其取值范围为最优解不变的范围,即不突破构成最优解的两条直线斜率kmin和kmax的范围。2、求解时,将目标函数变换为x2=(-c1/c2)*x1的形式,通过kmin≤(-c1/c2)≤kmax,分别代入c1或c2,可得c2或c1的上、下限。E、约束条件常数项的上、下限1、约束条件常数项的变化,在图解时可视为约束条件直线在纵轴上截距的变动,即该直线沿横轴平移,不会与另两条约束条...