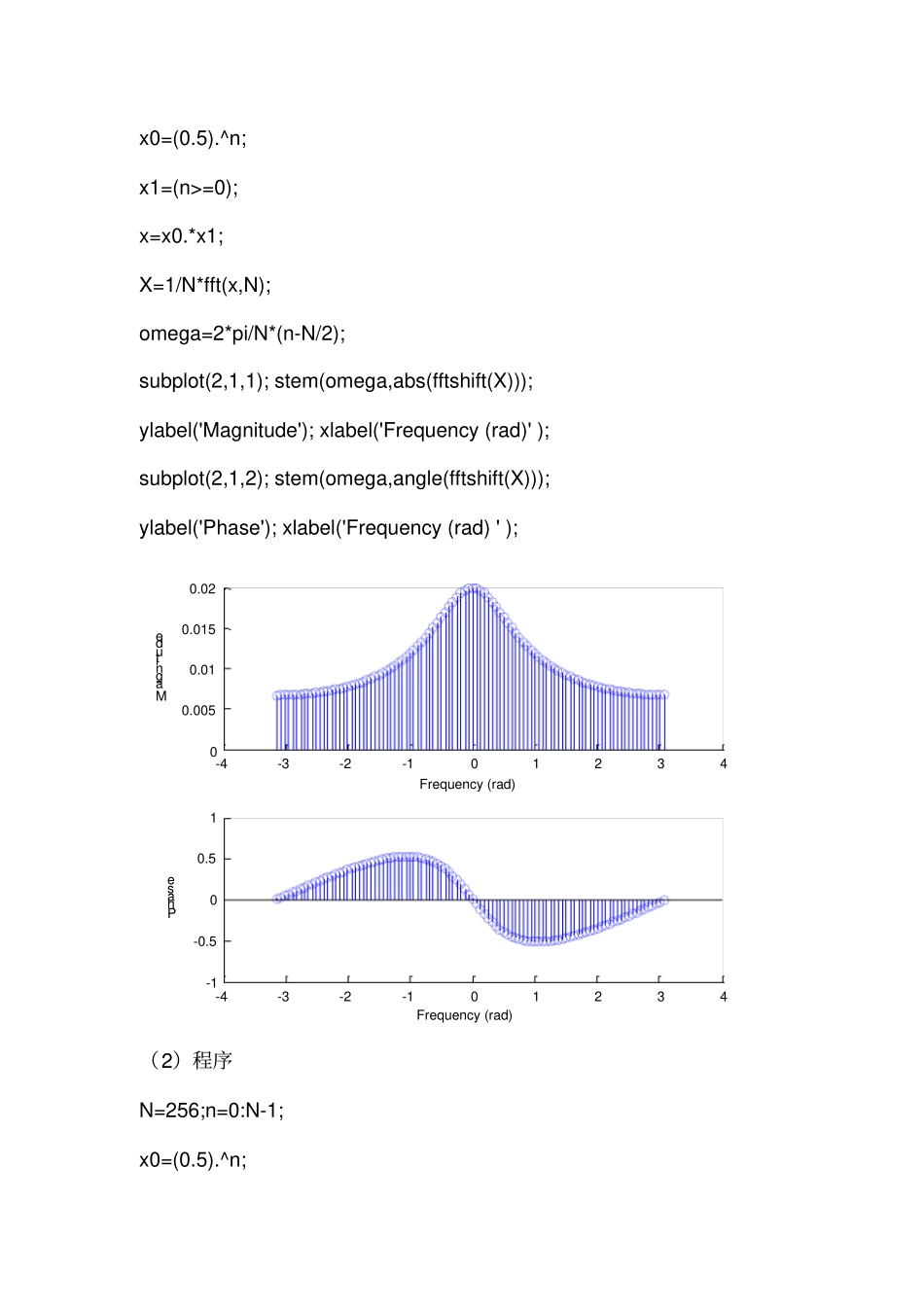
一、利用DFT分析离散序列频谱应用傅里叶变换DFT,分析各种离散序列x(n)的频谱。离散周期信号的分析离散周期信号可以展开成离散傅里叶级数,102)(~.1)(~NkknNjekXNnx其中傅里叶系数)(~kX如下所示:102)(~.)(~NnknNjenxkX式中:N是序列的周期,n为时间离散变量,k为数字频率离散变量,是k次谐波的数字频率。所以离散周期信号的频谱X(k)是一个以N为周期的周期性离散频谱,各谱线之间的间隔为ω0=2π/N,而且存在着谐波的关系。离散周期序列在时域与频域都是离散的、以N为周期的序列。正确地在一个周期内选取N,即可以准确地求取周期序列的频谱。离散周期序列频谱的求解步骤:(1)确定离散周期序列的基本周期N;(2)使用fft命令作N点FFT计算。频率分辨率F0=2π/N(3)令X(kω0)=1/NX(k)。1.利用DFT计算序列)(21)(nunxn的频谱(1)程序N=100;n=0:N-1;x0=(0.5).^n;x1=(n>=0);x=x0.*x1;X=1/N*fft(x,N);omega=2*pi/N*(n-N/2);subplot(2,1,1);stem(omega,abs(fftshift(X)));ylabel('Magnitude');xlabel('Frequency(rad)');subplot(2,1,2);stem(omega,angle(fftshift(X)));ylabel('Phase');xlabel('Frequency(rad)');-4-3-2-10123400.0050.010.0150.02MagnitudeFrequency(rad)-4-3-2-101234-1-0.500.51PhaseFrequency(rad)(2)程序N=256;n=0:N-1;x0=(0.5).^n;x1=(n>=0);x=x0.*x1;X=1/N*fft(x,N);omega=2*pi/N*(n-N/2);subplot(2,1,1);stem(omega,abs(fftshift(X)));ylabel('Magnitude');xlabel('Frequency(rad)');subplot(2,1,2);stem(omega,angle(fftshift(X)));ylabel('Phase');xlabel('Frequency(rad)');-4-3-2-10123402468x10-3MagnitudeFrequency(rad)-4-3-2-101234-1-0.500.51PhaseFrequency(rad)(3)程序N=300;n=0:N-1;x0=(0.5).^n;x1=(n>=0);x=x0.*x1;X=1/N*fft(x,N);omega=2*pi/N*(n-N/2);subplot(2,1,1);stem(omega,abs(fftshift(X)));ylabel('Magnitude');xlabel('Frequency(rad)');subplot(2,1,2);stem(omega,angle(fftshift(X)));ylabel('Phase');xlabel('Frequency(rad)');-4-3-2-10123402468x10-3MagnitudeFrequency(rad)-4-3-2-101234-1-0.500.51PhaseFrequency(rad)二、连续系统的分析零输入、零状态法求解系统的响应MATLAB的控制工具箱(controltoolbox)里包含了许多可用于分析线性时不变(LTI)系统的函数,使用命令helpcontrol可以查看控制工具箱里的这些函数。对于线性时不变的连续系统,在时域中其数学模型用常系数线性微分方程来描述。如下:)()()(0)(0txbtyajMjjiNii在拉普拉斯变换中,可用系统函数H(s)来描述,且根据其零,极点的分布情况,可以决定系统的结构及系统的稳定性。NiiiMjjjsasbsH00)(另外还可以用状态变量分析法进行系统描述。此设计完成用Matlab实现几种分析方法的相互转换。在Matlab中,描述系统的传递函数(系统函数)型tf(transferfunction),零极点型zp(zeropole)以及状态变量型ss(statespace)三种方式可以方便的转换。Matlab相应的语句为:tf2zp——系统函数型转换到零极点型tf2ss——系统函数型转换到状态变量型zp2tf——零极点型转换到系统函数型zp2ss——零极点型转换到状态变量型ss2tf——状态变量型转换到系统函数型ss2zp——状态变量型转换到零极点型1:已知一个因果LTI离散系统的系统函数为:)2(0675.0)1(1349.0)(0675.0)2(4128.0)1(143.1)(nxnxnxnynyny(1)阶跃响应M=30;N=32;omega=[0:(N-1)]*2*pi/N;H=(0.0675+0.1349*exp(-j.*omega)+0.0675*exp(-2*j.*omega))./(1-1.143*exp(-j.*omega)+0.4128*exp(-2*j.*omega));x=ones(1,M);X=fft(x,N);Y=X.*H;y=ifft(Y,N);figure(1);subplot(2,1,1);stem([0:M-1],x);xlabel('Timeindexn');ylabel('x[n]');title('Inputsignalandoutputsignal');subplot(2,1,2);stem([0:M-1],real(y(1:M)));xlabel('Timeindexn');ylabel('y[n]');05101520253000.51Timeindexnx[n]Inputsignalandoutputsignal05101520253000.511.5Timeindexny[n](2)单位脉冲响应h(n)M=30;N=32;omega=[0:(N-1)]*2*pi/N;H=(0.0675+0.1349*exp(-j.*omega)+0.0675*exp(-2*j.*omega))./(1-1.143*exp(-j.*omega)+0.4128*exp(-2*j.*...