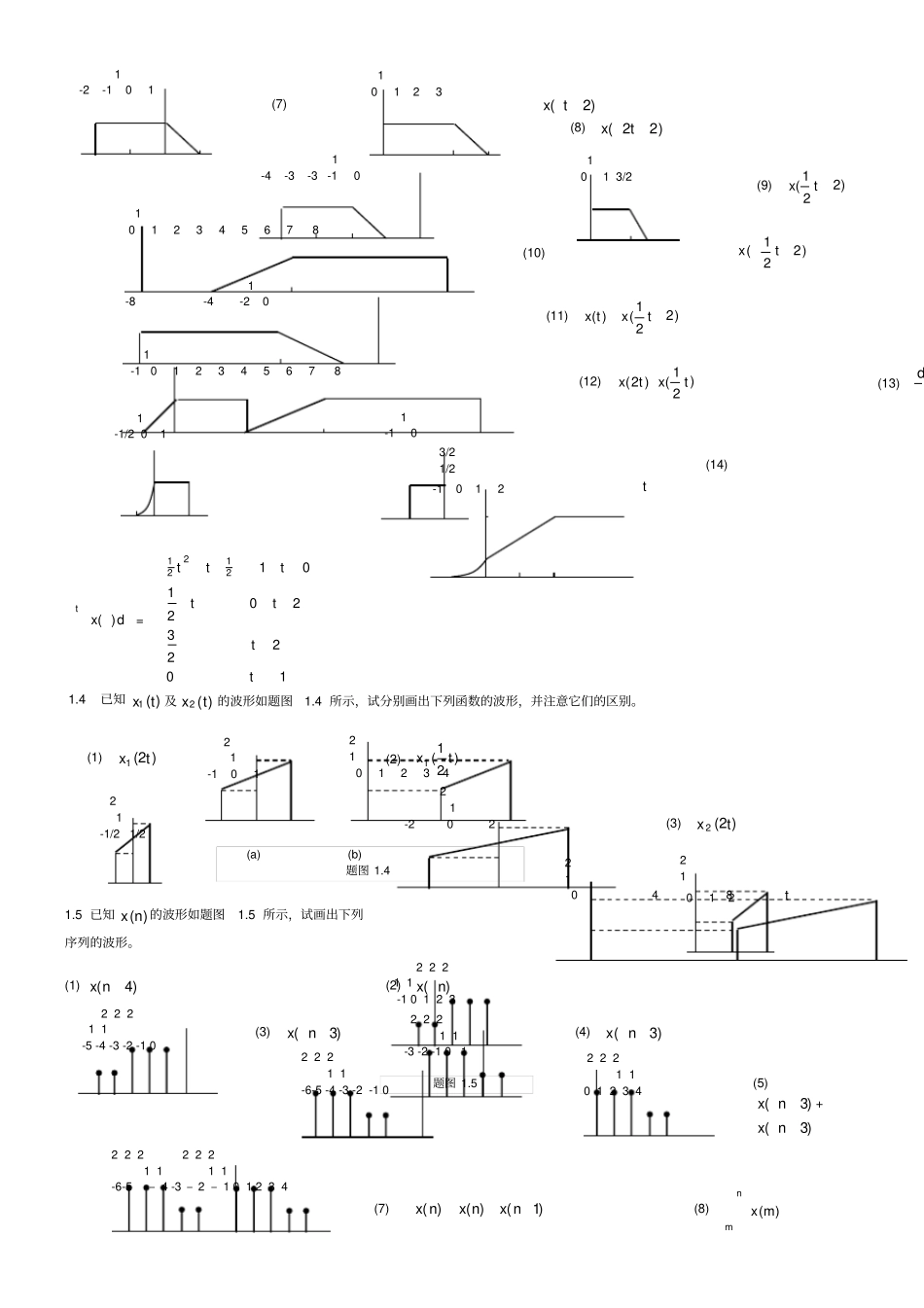
第一章习题参考解答1.1绘出下列函数波形草图。(1)||3)(tetx(2)02021)(nnnxnn(3))(2sin)(tttx(4))(4sin)(nnnx(5))]4()([4cos)(tttetxt(6))]4()1([3)(nnnxn(7)ttttx2cos)]2()([)((8))]1()3([)(nnnnx(9))2()1(2)()(ttttx(10))5(5)]5()([)(nnnnnx(11))]1()1([)(ttdtdtx(12))()5()(nnnx(13)tdtx)1()((14))()(nnnx1.2确定下列信号的能量和功率,并指出是能量信号还是功率信号,或两者均不是。(1)||3)(tetx解能量有限信号。信号能量为:(2)02021)(nnnxnn解能量有限信号。信号能量为:(3)ttx2sin)(解功率有限信号。周期信号在(,)区间上的平均功率等于在一个周期内的平均功率,t2sin的周期为1。(4)nnx4sin)(解功率有限信号。n4sin是周期序列,周期为8。(5))(2sin)(tttx解功率有限信号。由题(3)知,在),(区间上t2sin的功率为1/2,因此)(2sintt在),(区间上的功率为1/4。如果考察)(2sintt在),0(区间上的功率,其功率为1/2。(6))(4sin)(nnnx解功率有限信号。由题(4)知,在),(区间上n4sin的功率为1/2,因此)(4sinnn在),(区间上的功率为1/4。如果考察)(4sinnn在),0(区间上的功率,其功率为1/2。(7)tetx3)(解非功率、非能量信号。考虑其功率:上式分子分母对T求导后取极限得P。(8))(3)(tetxt解能量信号。信号能量为:1.3已知)(tx的波形如题图1.3所示,试画出下列函数的波形。(1))2(tx(2))2(tx(3))2(tx(4)(x(5))(tx(6))2(tx-3-2-1012300.51n(2)......1-1012题图1.31-3-2-101012341-1/2011-2-101234(7))2(tx(8))22(tx(9))221(tx)221(tx(10)(11))221()(txtx(12))21()2(txtx(13)d(14)tdx)(=1022320210121221ttttttt1.4已知)(1tx及)(2tx的波形如题图1.4所示,试分别画出下列函数的波形,并注意它们的区别。(1))2(1tx(2))21(1tx(3))2(2tx1.5已知)(nx的波形如题图1.5所示,试画出下列序列的波形。(1))4(nx(2))(nx(3))3(nx(4))3(nx(5))3(nx+)3(nx(7))1()()(nxnxnx(8)nmmx)(21-1012101234(a)(b)题图1.41-2-101101231-4-3-3-101013/21-8-4-2010123456781-10123456781-1/2011-103/21/2-1012t21-1/21/221012t21-2022104822211-10123题图1.522211-3-2-10122211-5-4-3-2-1022211-6-5-4-3-2-1022211012342222221111-6-5–4-3–2–1012341.6任何信号可以分解为奇分量和偶分量的和:)()()(txtxtxoe或)()()(nxnxnxoe其中ex为偶分量;ox为奇分量。偶分量和奇分量可以由下式确定:)]()([21)(txtxtxe,)]()([21)(txtxtxo)]()([21)(nxnxnxe,)]()([21)(nxnxnxo(1)试证明)()(txtxee或)()(nxnxee;)()(txtxoo或)()(nxnxoo。(2)试确定题图1.6(a)和(b)所示信号的偶分量和奇分量,并绘出其波形草图。(1)证明根据偶分量和奇分量的定义:离散序列的证明类似。(2)根据定义可绘出下图1.7设nnx2)(,试求)(),(),(),(22nxnxnxnx。11222122)1()()(nnnnnxnxnx解1.8判断下列信号是否为周期信号,若是周期的,试求其最小周期。(1))64cos()(ttx解周期信号,21T(2))()2sin()(tttx解非周期信号。(3))2cos()(tetxt解非周期信号。(4))3(4)(tjetx解周期信号,81T。(5))cos()5sin()(tbtatx解若,0,0ba则)(tx为周期信号,21bT;若,0,0ba则)(tx为周期信号,521aT;若,0,0ba则)(tx为非周期信号。(6))38cos()(nnx解周期信号,161N。(7))97cos()(nnx解周期信号,181N。(8))16()(nconnx解:非周期信号。11-4n-10123-2888642⋯1-1012345101221123n-2-10-1-2-3(a)(b)题图1.610121-2-101/2-2-10121/2-2-1012t21123n-2-10-1-2-321-3-2-1012n-1-2-3-330n-3/2-3/2-3/221123-3-2-10n-1-2-3/2(9)njenx152)(解:周期信号,151N。(10))34sin(2)3sin()6cos(3)(nnnnx解:周期信号,最小公共周期为241N。1.9计算下列各式的值。(1)dttttx)()(0解:原式dtttx)()(0=).(0tx(2)tdtx)()(0解:原式dtxt)()(0)()(0ttx(3)dttttx)()(0解:原式dtttx)()(0)(0tx(4)dttttx)(')(0解:原式)(')(000'txttxt(5)dttttt)2()(00解:原式dttttt)()2(000)2(0t(6)tdtt)2()(00解:原式=tdttt)2()(000=tdtt)()(00)()(00ttt=0)(00000tttt(7)dtt)(解:原式1(8)0)(dtt解:原式0(9)0)(dtt解原式0(10)00)(dtt解原式1(11)dtttt)12)(33(2解令tv3得:原式dvvvv31]132)3)[(3(232]132)3[(31xvv32(12)dttxt)()1('解:原...