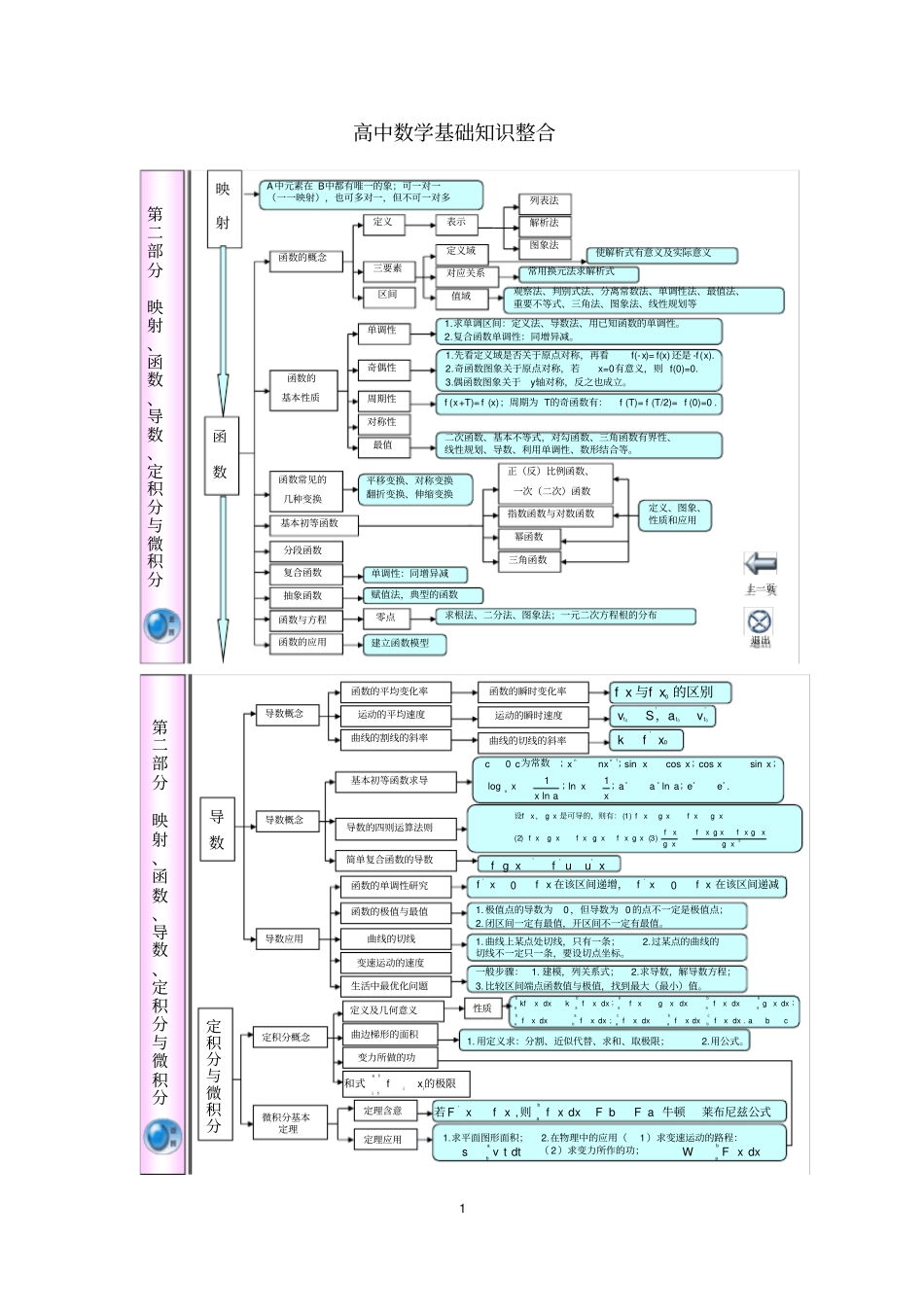
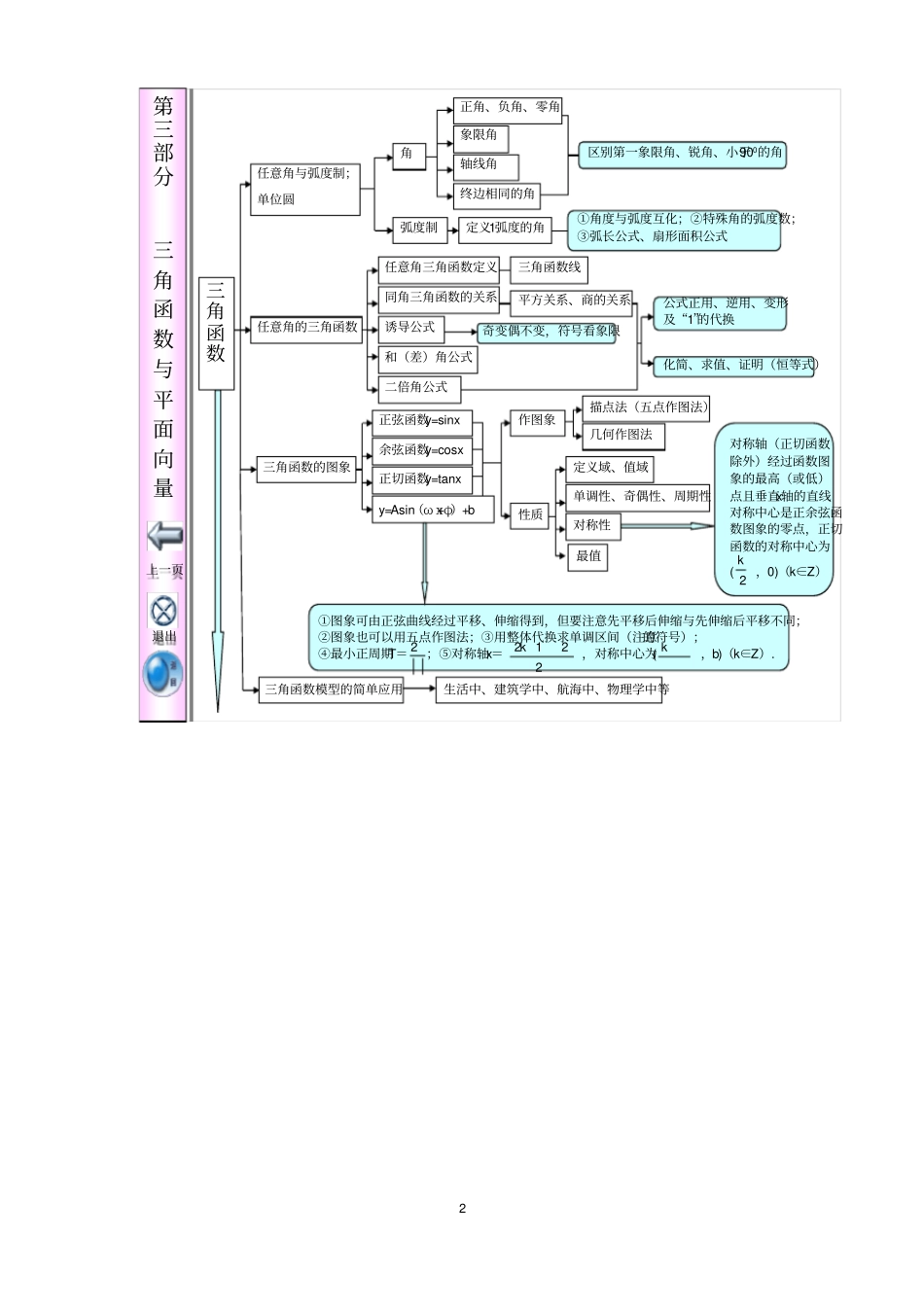
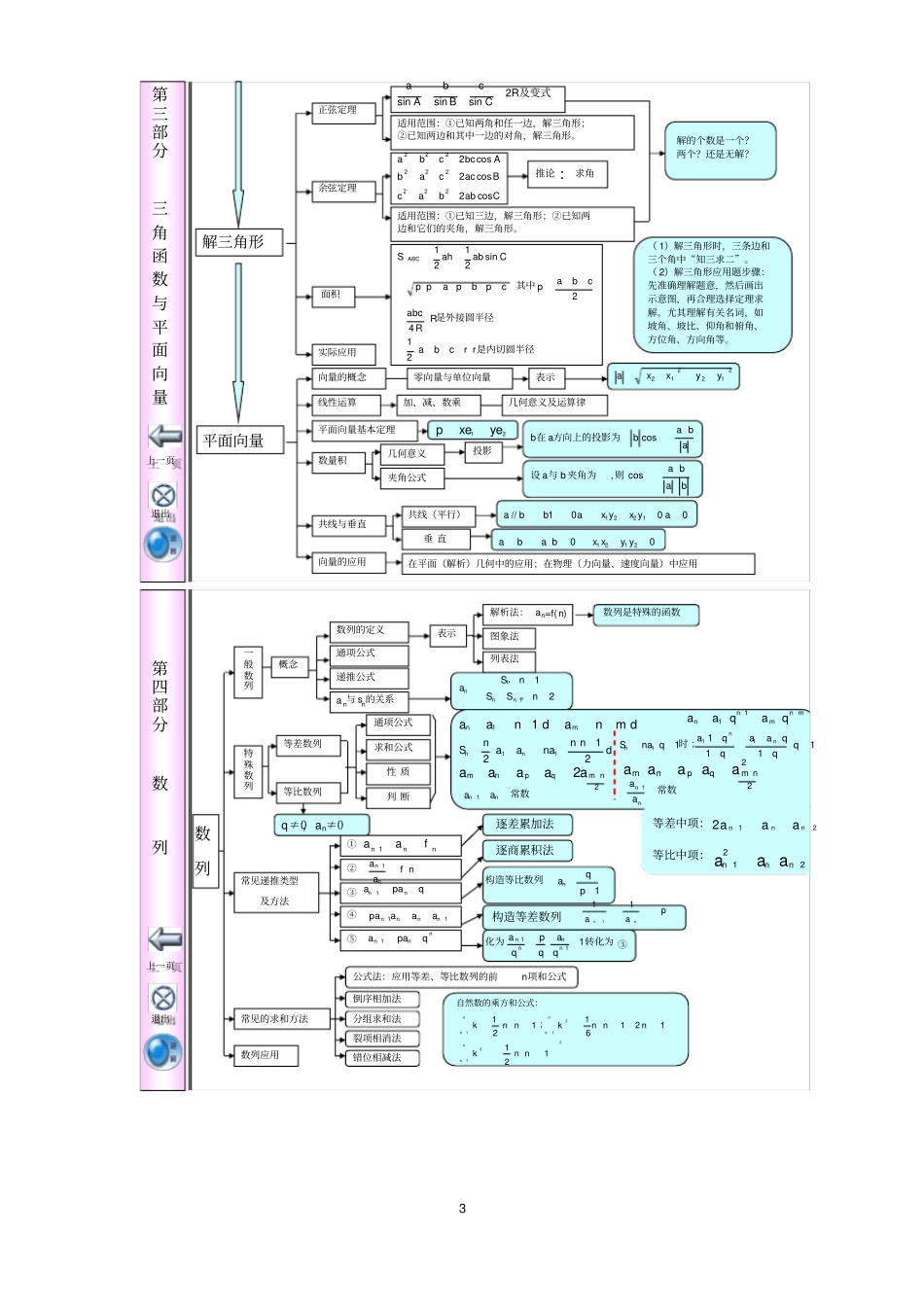
1高中数学基础知识整合函数与方程区间建立函数模型抽象函数复合函数分段函数求根法、二分法、图象法;一元二次方程根的分布单调性:同增异减赋值法,典型的函数零点函数的应用A中元素在B中都有唯一的象;可一对一(一一映射),也可多对一,但不可一对多函数的基本性质单调性奇偶性周期性对称性最值1.求单调区间:定义法、导数法、用已知函数的单调性。2.复合函数单调性:同增异减。1.先看定义域是否关于原点对称,再看f(-x)=f(x)还是-f(x).2.奇函数图象关于原点对称,若x=0有意义,则f(0)=0.3.偶函数图象关于y轴对称,反之也成立。f(x+T)=f(x);周期为T的奇函数有:f(T)=f(T/2)=f(0)=0.二次函数、基本不等式,对勾函数、三角函数有界性、线性规划、导数、利用单调性、数形结合等。函数的概念定义列表法解析法图象法表示三要素使解析式有意义及实际意义常用换元法求解析式观察法、判别式法、分离常数法、单调性法、最值法、重要不等式、三角法、图象法、线性规划等定义域对应关系值域函数常见的几种变换平移变换、对称变换翻折变换、伸缩变换基本初等函数正(反)比例函数、一次(二次)函数幂函数指数函数与对数函数三角函数定义、图象、性质和应用函数映射第二部分映射、函数、导数、定积分与微积分退出上一页第二部分映射、函数、导数、定积分与微积分导数导数概念函数的平均变化率运动的平均速度曲线的割线的斜率函数的瞬时变化率运动的瞬时速度曲线的切线的斜率的区别与0xfxf''000tttvaSv,0'xfk导数概念基本初等函数求导导数的四则运算法则简单复合函数的导数.ln1lnln1logsincoscossin01xxxxanneeaaaxxaxxxxxxnxxcc;;;;;;;为常数2)3()2()1(xgxgxfxgxfxgxfxgxfxgxfxgxfxgxfxgxfxgxf是可导的,则有:,设xuufxgf'''1.极值点的导数为0,但导数为0的点不一定是极值点;2.闭区间一定有最值,开区间不一定有最值。导数应用函数的单调性研究函数的极值与最值曲线的切线变速运动的速度生活中最优化问题.00''在该区间递减在该区间递增,xfxfxfxf1.曲线上某点处切线,只有一条;2.过某点的曲线的切线不一定只一条,要设切点坐标。一般步骤:1.建模,列关系式;2.求导数,解导数方程;3.比较区间端点函数值与极值,找到最大(最小)值。定积分与微积分定积分概念定理应用性质定理含意微积分基本定理曲边梯形的面积变力所做的功的极限和式iniixf11定义及几何意义1.用定义求:分割、近似代替、求和、取极限;2.用公式。cbadxxfdxxfdxxfdxxfdxxfdxxgdxxfdxxgxfdxxfkdxxkfcbbacaabbabababababa.;;;莱布尼兹公式牛顿则若aFbFdxxfxfxFba,'1.求平面图形面积;2.在物理中的应用(1)求变速运动的路程:(2)求变力所作的功;badxxFWdttvsab2第三部分三角函数与平面向量退出上一页化简、求值、证明(恒等式)任意角的三角函数任意角三角函数定义同角三角函数的关系诱导公式和(差)角公式二倍角公式三角函数线平方关系、商的关系奇变偶不变,符号看象限公式正用、逆用、变形及“1”的代换角正角、负角、零角象限角轴线角终边相同的角区别第一象限角、锐角、小于900的角任意角与弧度制;单位圆弧度制定义1弧度的角①角度与弧度互化;②特殊角的弧度数;③弧长公式、扇形面积公式正弦函数y=sinx三角函数的图象余弦函数y=cosx正切函数y=tanxy=Asin(ωx+φ)+b作图象描点法(五点作图法)几何作图法性质定义域、值域单调性、奇偶性、周期性对称性最值对称轴(正切函数除外)经过函数图象的最高(或低)点且垂直x轴的直线对称中心是正余弦函数图象的零点,正切函数的对称中心为(,0)(k∈Z)2k①图象可由正弦曲线经过平移、伸缩得到,但要注意先平移后伸缩与先伸缩后平移不同;②图象也可以用五点作图法;③用整体代换求单调区间(注意的符号);④最小正周期T=;⑤对称轴x=,对称中心为(,b)(k∈Z).22212kk三角函数三角函数模型的简单应用生活中、建筑学中、航海中、物理学中等3第三部分三角函数与平面向量退出上一页(1)解三角形时,三条边和三个角中“知三求二”。(2)解三角形应用题步骤:先准确理解题意,然后画出示意图,再合理选择定理求解。尤其理解有关名词,如坡角、坡比、...