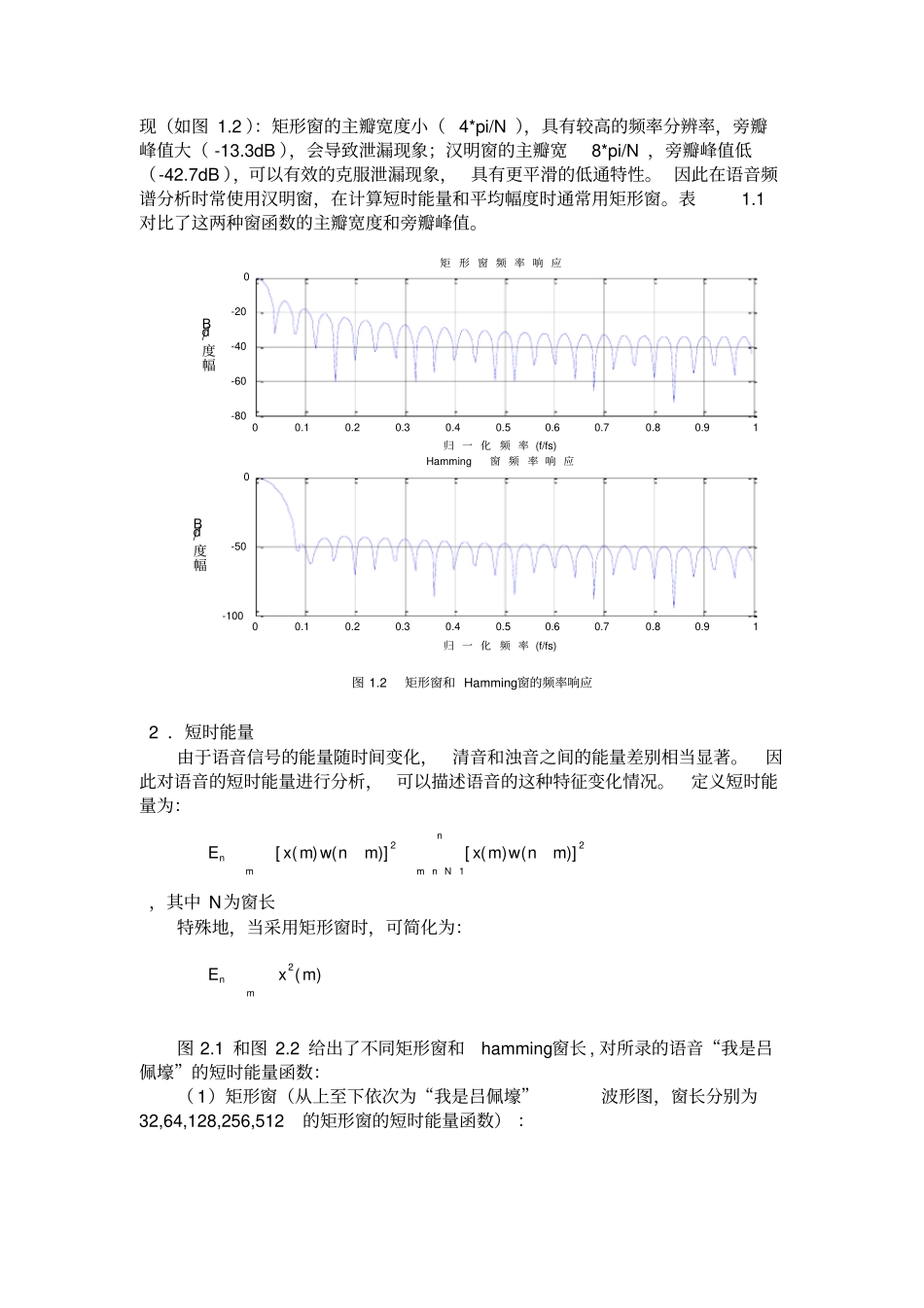
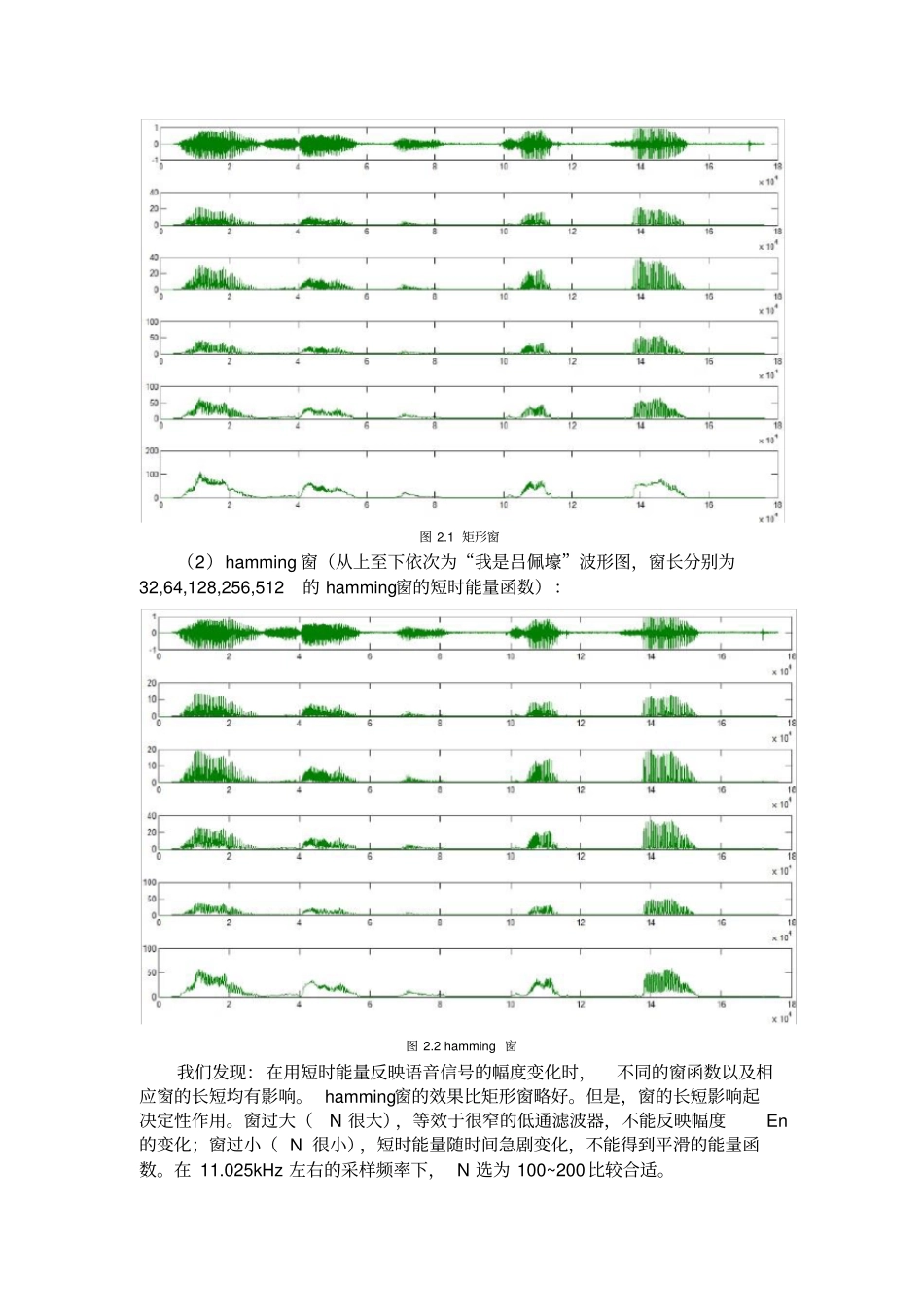
数字语音实验吕佩壕10024134一、实验要求1.编程实现一句话语音的短时能量曲线,并比较窗长、窗口形状(以直角窗和和哈明窗为例)对短时平均能量的影响;2.编程分析语音信号的短时谱特性,并比较窗长、窗口形状(以直角窗和和哈明窗为例)对语音短时谱的影响;3.运用低通滤波器、中心削波和自相关技术估计一段男性和女性语音信号的基音周期,画出基音轨迹曲线,给出估计准确率。二、实验原理及实验结果1.窗口的选择通过对发声机理的认识,语音信号可以认为是短时平稳的。在5~50ms的范围内,语音频谱特性和一些物理特性参数基本保持不变。我们将每个短时的语音称为一个分析帧。一般帧长取10~30ms。我们采用一个长度有限的窗函数来截取语音信号形成分析帧。通常会采用矩形窗和汉明窗。图1.1给出了这两种窗函数在窗长N=50时的时域波形。图1.1矩形窗和hamming窗的时域波形矩形窗的定义:一个N点的矩形窗函数定义为如下:1,00,()nNwn其他Hamming窗的定义:一个N点的hamming窗函数定义为如下:0.540.46cos(2),010,()nnNNwn其他=这两种窗函数都有低通特性,通过分析这两种窗的频率响应幅度特性可以发020406000.20.40.60.811.21.41.61.82矩形窗samplew(n)020406000.10.20.30.40.50.60.70.80.91hanming窗samplew(n)现(如图1.2):矩形窗的主瓣宽度小(4*pi/N),具有较高的频率分辨率,旁瓣峰值大(-13.3dB),会导致泄漏现象;汉明窗的主瓣宽8*pi/N,旁瓣峰值低(-42.7dB),可以有效的克服泄漏现象,具有更平滑的低通特性。因此在语音频谱分析时常使用汉明窗,在计算短时能量和平均幅度时通常用矩形窗。表1.1对比了这两种窗函数的主瓣宽度和旁瓣峰值。图1.2矩形窗和Hamming窗的频率响应2.短时能量由于语音信号的能量随时间变化,清音和浊音之间的能量差别相当显著。因此对语音的短时能量进行分析,可以描述语音的这种特征变化情况。定义短时能量为:221[()()][()()]nnmmnNExmwnmxmwnm,其中N为窗长特殊地,当采用矩形窗时,可简化为:2()nmExm图2.1和图2.2给出了不同矩形窗和hamming窗长,对所录的语音“我是吕佩壕”的短时能量函数:(1)矩形窗(从上至下依次为“我是吕佩壕”波形图,窗长分别为32,64,128,256,512的矩形窗的短时能量函数):00.10.20.30.40.50.60.70.80.91-80-60-40-200矩形窗频率响应归一化频率(f/fs)幅度/dB00.10.20.30.40.50.60.70.80.91-100-500Hamming窗频率响应归一化频率(f/fs)幅度/dB图2.1矩形窗(2)hamming窗(从上至下依次为“我是吕佩壕”波形图,窗长分别为32,64,128,256,512的hamming窗的短时能量函数):图2.2hamming窗我们发现:在用短时能量反映语音信号的幅度变化时,不同的窗函数以及相应窗的长短均有影响。hamming窗的效果比矩形窗略好。但是,窗的长短影响起决定性作用。窗过大(N很大),等效于很窄的低通滤波器,不能反映幅度En的变化;窗过小(N很小),短时能量随时间急剧变化,不能得到平滑的能量函数。在11.025kHz左右的采样频率下,N选为100~200比较合适。短时能量函数的应用:1)可用于区分清音段与浊音段。En值大对应于浊音段,En值小对应于清音段。2)可用于区分浊音变为清音或清音变为浊音的时间(根据En值的变化趋势)。3)对高信噪比的语音信号,也可以用来区分有无语音(语音信号的开始点或终止点)。无信号(或仅有噪声能量)时,En值很小,有语音信号时,能量显著增大。Matlab程序:figure(3);a=wavread('C:\audio.wav');subplot(6,1,1),plot(a);N=32;fori=2:6h=rectwin(2.^(i-2)*N);b=a.*a;En=conv2(h,b);%求短时能量函数Ensubplot(6,1,i),plot(En);i=i+1;if(i==2)legend('N=32');elseif(i==3)legend('N=64');elseif(i==4)legend('N=128');elseif(i==5)legend('N=256');elseif(i==6)legend('N=512');endendfigure(4);a=wavread('C:\audio.wav');subplot(6,1,1),plot(a);N=32;fori=2:6h=hamming(2.^(i-2)*N);%形成一个汉明窗,长度为2.^(i-2)*Nb=a.*a;En=conv2(h,b);%求短时能量函数Ensubplot(6,1,i),plot(En);i=i+1;if(i==2)legend('N=32');elseif(i==3)legend('N=64');elseif(i==4)legend('N=128');elseif(i==5)legend('N=25...