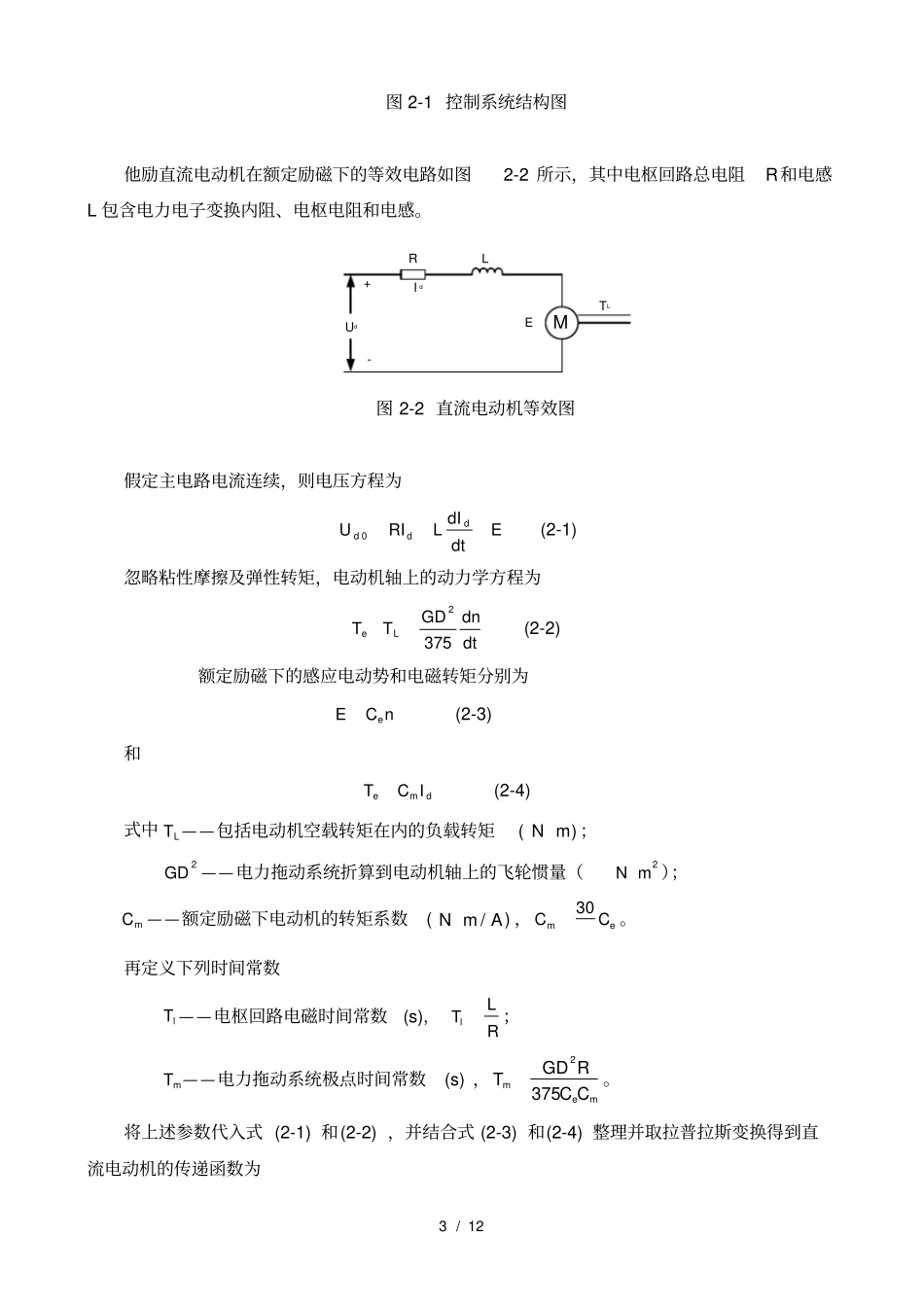
1/12基于MATLAB的直流调速数字控制系统的分析和设计电气与信息工程学院自动化13-2马春野2/12基于MATLAB的直流调速数字控制系统的分析和设计摘要:本文简单介绍了直流调速系统数字控制的特点和直流调速系统模型的建立,重点介绍了数字PI控制器和利用Z域根轨迹的设计方法,以及用MATLAB进行了设计过程的仿真和稳定性、动态特性的分析。关键词:直流调速;数字PI控制器;Z域根轨迹法;MATLAB仿真1引言随着计算机技术的发展,直流调速系统的数字化控制已得到广泛应用。较之用传统的用模拟电路实现直流调速系统的触发和调节,数字调节器有着明显的优势。即用微机执行数字PID运算程序代替模拟转速调节器和电流调节器,而转速给定、转速反馈和电流反馈经A/D转换器变成数字量送入微机(或单片机),微机的运算结果通过D/A转换器变成模拟量作为可控整流装置的触发控制电压。这种方式不但克服了电网电压波动对触发精度的影响,而且在一定程度上也减小了因器件老化、网压和温度变化引起的运算误差。由于计算机具有高精度、高速度和编程灵活等优点,可以在系统中灵活的使用各种算法实现最优控制;并且对控制结果的观察更加明确,对控制结果的分析也可以在显示器上绘制曲线来表示[1]。计算机控制系统的经典设计方法一般分为两种。一种是将连续域设计好的控制律D(s)利用不同的离散化方法变换为离散控制律D(z),这种方法称为“连续域—离散化设计”方法,他允许设计师利用熟悉的各种连续域设计方法设计出令人满意的连续域控制器,然后将控制器离散化,离散化过程较为简单。另一种方法是在离散域先建立被控对象的离散模型G(z),然后直接在离散域进行控制器设计。2系统数学模型的建立系统的结构图如图2-1所示数数数数数PWM数数数数数数数数数数数数数数数_3/12图2-1控制系统结构图他励直流电动机在额定励磁下的等效电路如图2-2所示,其中电枢回路总电阻R和电感L包含电力电子变换内阻、电枢电阻和电感。Ud-RL+ETLMId图2-2直流电动机等效图假定主电路电流连续,则电压方程为0ddddIURILEdt(2-1)忽略粘性摩擦及弹性转矩,电动机轴上的动力学方程为2375eLGDdnTTdt(2-2)额定励磁下的感应电动势和电磁转矩分别为eECn(2-3)和emdTCI(2-4)式中LT——包括电动机空载转矩在内的负载转矩(Nm);2GD——电力拖动系统折算到电动机轴上的飞轮惯量(2Nm);mC——额定励磁下电动机的转矩系数(/NmA),30meCC。再定义下列时间常数lT——电枢回路电磁时间常数(s),lLTR;mT——电力拖动系统极点时间常数(s),2375memGDRTCC。将上述参数代入式(2-1)和(2-2),并结合式(2-3)和(2-4)整理并取拉普拉斯变换得到直流电动机的传递函数为4/12021/()1mlmCeGsTTsTs(2-5)整流装置采用IGBT三相桥式整流电路,用PWM来控制。PWM控制的整流装置和晶闸管触发的动态数学模型基本一致,是一个滞后环节,其传递函数可以写成1()sTsSGsKe(2-6)由于时间常数sT非常小,所以对式(2-6)进行泰勒展开,近似等效成一个一阶惯性环节,即1()1SsKGsTs(2-7)将转速反馈系数折算到前向通道,给定值为原来的1/倍,则直流调速系统的开环传递函数为2/()(1)(1)SesmlmKCGsTsTTsTs(2-8)直流调速系统的实际参数具体如下:转速反馈系数=0.0158,机电时间常数mT=0.075s,电磁时间常数lT=0.017s,IGBT开关频率为10Hz,则sT=0.1ms。将上述参数代入式(2-8)得22.647()(0.000011)(0.0012750.0751)Gssss(2-9)由于IGBT整流装置的时间常数sT很小,可以忽略,则式(2-9)可以近似为22.647()(0.0012750.0751)Gsss(2-10)3控制系统的设计和仿真3.1采样周期的选择在计算机控制系统里,采样周期T是系统的一个重要的参数,对闭环系统的稳定性和性能有很大的影响。一般的,采样周期越小,稳定性越好,但采样周期太小时,由于计算机运算部件、A/D和D/A变换器的字长有限,计算机控制系统并不趋于连续系统,且由于字长有限所产生的量化误差会增大。同时,采样周期过小时,将会增大控制算法对参数变化的灵敏度,使控制算法参数不能准确表示,从而使控制算法的特性变化较大。所以要考虑不同的因素,选取一个合适的采样周期。为了减少频率混叠现象,选择采样频率时,常常要求采样频率满足max(4~10)s...