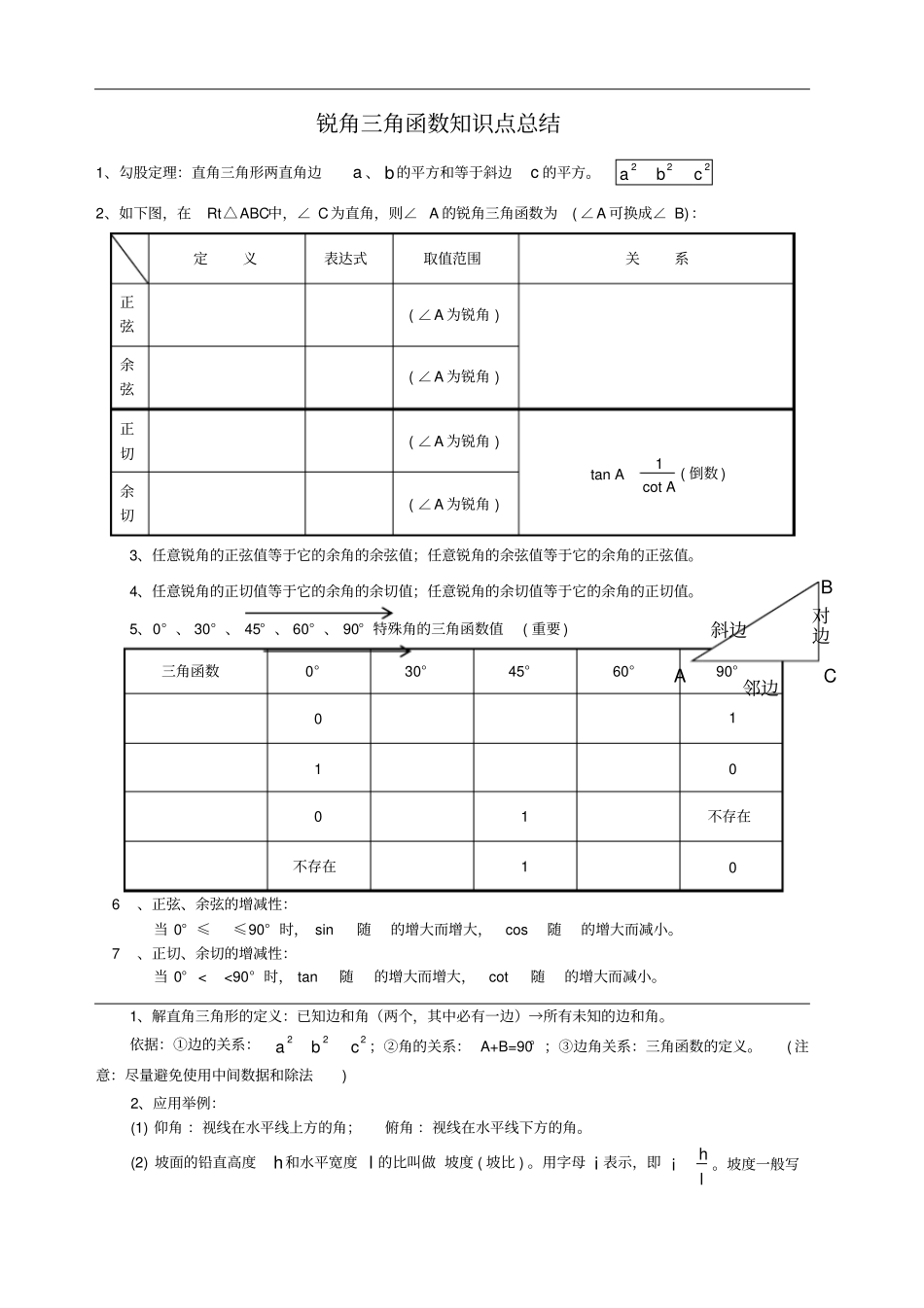
锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平方。222cba2、如下图,在Rt△ABC中,∠C为直角,则∠A的锐角三角函数为(∠A可换成∠B):定义表达式取值范围关系正弦(∠A为锐角)余弦(∠A为锐角)正切(∠A为锐角)AAcot1tan(倒数)余切(∠A为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)三角函数0°30°45°60°90°011001不存在不存在106、正弦、余弦的增减性:当0°≤≤90°时,sin随的增大而增大,cos随的增大而减小。7、正切、余切的增减性:当0°<<90°时,tan随的增大而增大,cot随的增大而减小。1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。依据:①边的关系:222cba;②角的关系:A+B=90°;③边角关系:三角函数的定义。(注意:尽量避免使用中间数据和除法)2、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。(2)坡面的铅直高度h和水平宽度l的比叫做坡度(坡比)。用字母i表示,即hil。坡度一般写对边邻边斜边ACB成1:m的形式,如1:5i等。把坡面与水平面的夹角记作(叫做坡角),那么tanhil。3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。如图3,OA、OB、OC、OD的方向角分别是:45°、135°、225°。4、指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角。如图4,OA、OB、OC、OD的方向角分别是:北偏东30°(东北方向),南偏东45°(东南方向),南偏西60°(西南方向),北偏西60°(西北方向)。反比例函数知识点整理一、反比例函数的概念1、解析式:0kxky其他形式:①kxy②1kxy例1.下列等式中,哪些是反比例函数(1)3xy(2)xy2(3)xy=21(4)25xy(5)xy23(6)31xy(7)y=x-4例2.当m取什么值时,函数23)2(mxmy是反比例函数?例3.若函数22)12(mxmy是反比例函数,且它的图像在第二、四象限,则m的值是___________例4.已知函数y=y1+y2,y1与x成正比例,y2与x成反比例,且当x=1时,y=4;当x=2时,y=5(1)求y与x的函数关系式(2)当x=-2时,求函数y的值2.反比例函数图像上的点的坐标满足:kxy例1.已知反比例函数的图象经过点(m,2)和(-2,3)则m的值为例2.下列函数中,图像过点M(-2,1)的反比例函数解析式是()例3.如果点(3,-4)在反比例函数kyx的图象上,那么下列各点中,在此图象上的是()A.(3,4)B.(-2,-6)C.(-2,6)D.(-3,-4)例4.如果反比例函数xky的图象经过点(3,-1),那么函数的图象应在()A.第一、三象限B.第二、四象限C.第一、二象限D.第三、四象限二、反比例函数的图像与性质1、基础知识0k时,图像在一、三象限,在每一个象限内,y随着x的增大而减小;0k时,图像在二、四象限,在每一个象限内,y随着x的增大而增大;例1.已知反比例函数yaxa()226,当x0时,y随x的增大而增大,求函数关系式例2.已知反比例函数xky12的图象在每个象限内函数值y随自变量x的增大而减小,且k的值还满足)12(29k≥2k-1,若k为整数,求反比例函数的解析式2、面积问题(1)三角形面积:kSAOB21例1.如图,过反比例函数xy1(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设△AOC和△BOD的面积分别是S1、S2,比较它们的大小,可得()(A)S1>S2(B)S1=S2(C)S1<S2(D)大小关系不能确定例2.如图,点P是反比例函数xy1的图象上任一点,PA垂直在x轴,垂足为pyOA,设OAP的面积为S,则S的值为例3.直线OA与反比例函数的图象在第一象限交于A点,AB⊥x轴于点B,若△OAB的面积为2,则k=.例4.如图,若点A在反比例函数(0)kykx的图象上,AMx轴于点M,AMO△的面积为3,则k.例5.如图,在x轴的正半轴上依次截取112233445OAAAAAAAAA,过点12345AAAAA、、、、分别作x轴的垂线与反比例函数的20yxx的图象相交于点12345PPPPP、、、、,得直角三角形1112233344455OPAAPAAPAAPAAPA2、、、、,并设其面积分别为12...