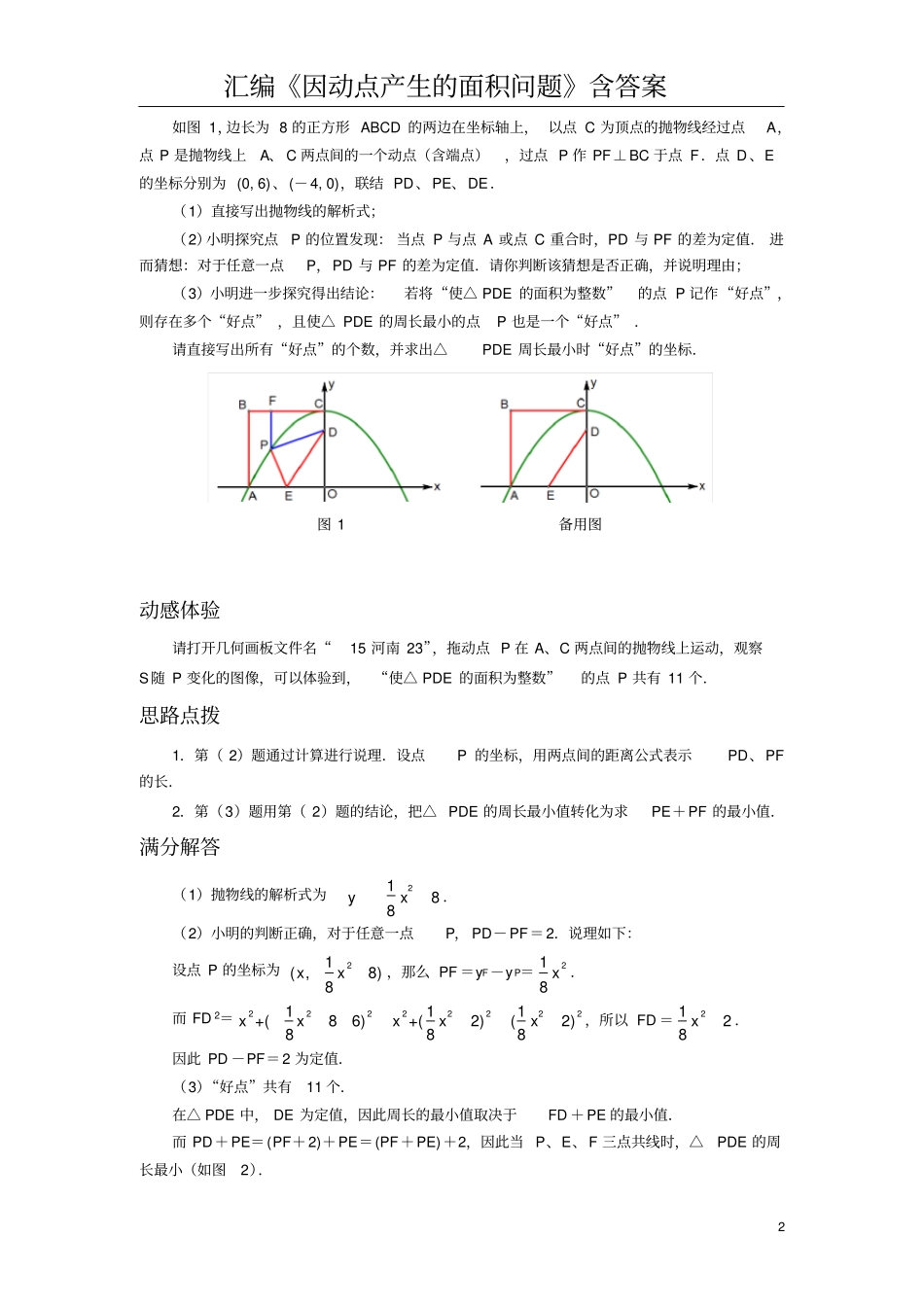
汇编《因动点产生的面积问题》含答案1例1如图1,边长为8的正方形ABCD的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上A、C两点间的一个动点(含端点),过点P作PF⊥BC于点F.点D、E的坐标分别为(0,6)、(-4,0),联结PD、PE、DE.(1)直接写出抛物线的解析式;(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值.进而猜想:对于任意一点P,PD与PF的差为定值.请你判断该猜想是否正确,并说明理由;(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE周长最小时“好点”的坐标.图1备用图汇编《因动点产生的面积问题》含答案2如图1,边长为8的正方形ABCD的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上A、C两点间的一个动点(含端点),过点P作PF⊥BC于点F.点D、E的坐标分别为(0,6)、(-4,0),联结PD、PE、DE.(1)直接写出抛物线的解析式;(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值.进而猜想:对于任意一点P,PD与PF的差为定值.请你判断该猜想是否正确,并说明理由;(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,则存在多个“好点”,且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE周长最小时“好点”的坐标.图1备用图动感体验请打开几何画板文件名“15河南23”,拖动点P在A、C两点间的抛物线上运动,观察S随P变化的图像,可以体验到,“使△PDE的面积为整数”的点P共有11个.思路点拨1.第(2)题通过计算进行说理.设点P的坐标,用两点间的距离公式表示PD、PF的长.2.第(3)题用第(2)题的结论,把△PDE的周长最小值转化为求PE+PF的最小值.满分解答(1)抛物线的解析式为2188yx.(2)小明的判断正确,对于任意一点P,PD-PF=2.说理如下:设点P的坐标为21(,8)8xx,那么PF=yF-yP=218x.而FD2=22222222111+(86)+(2)(2)888xxxxx,所以FD=2128x.因此PD-PF=2为定值.(3)“好点”共有11个.在△PDE中,DE为定值,因此周长的最小值取决于FD+PE的最小值.而PD+PE=(PF+2)+PE=(PF+PE)+2,因此当P、E、F三点共线时,△PDE的周长最小(如图2).汇编《因动点产生的面积问题》含答案3此时EF⊥x轴,点P的横坐标为-4.所以△PDE周长最小时,“好点”P的坐标为(-4,6).图2图3考点伸展第(3)题的11个“好点”是这样求的:如图3,联结OP,那么S△PDE=S△POD+S△POE-S△DOE.因为S△POD=1()32PODxx,S△POE=2111624POEyx,S△DOE=12,所以S△PDE=21316124xx=21344xx=21(6)134x.因此S是x的二次函数,抛物线的开口向下,对称轴为直线x=-6.如图4,当-8≤x≤0时,4≤S≤13.所以面积的值为整数的个数为10.当S=12时,方程21(6)13124x的两个解-8,-4都在-8≤x≤0范围内.所以“使△PDE的面积为整数”的“好点”P共有11个.图4汇编《因动点产生的面积问题》含答案4例2如图1,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于A(-2,0)、B(4,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P从点A出发,在线段AB上以每秒3个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ存在时,求运动多少秒时△PBQ的面积最大,最大面积是多少?(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK∶S△PBQ=5∶2,求点K的坐标.图1汇编《因动点产生的面积问题》含答案5如图1,在平面直角坐标系中,抛物线y=ax2+bx-3(a≠0)与x轴交于A(-2,0)、B(4,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P从点A出发,在线段AB上以每秒3个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ存在时,求运动多少秒时△PBQ的面积最大,最大面积是多...