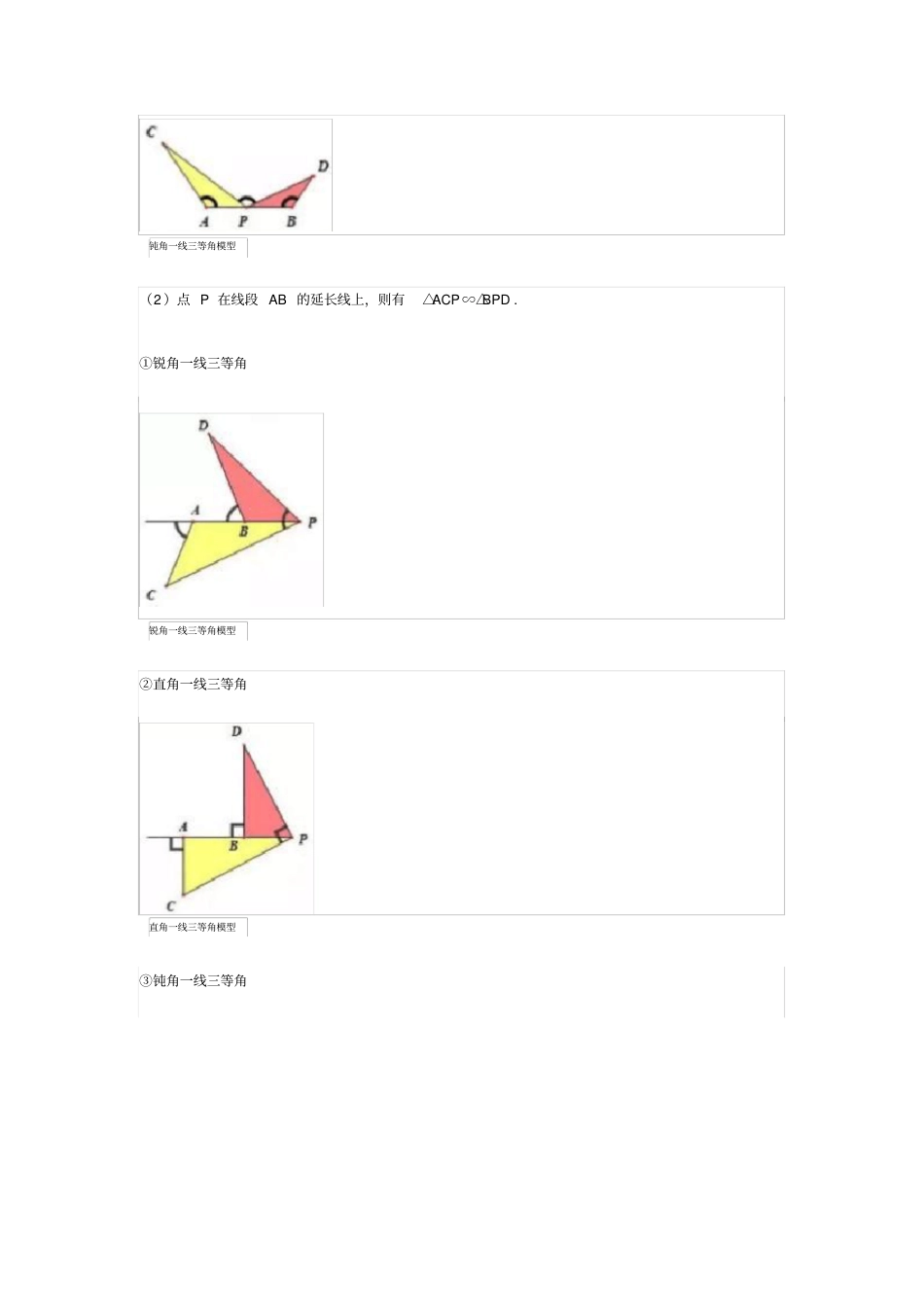
中考数学“一线三等角”模型解析一、“一线三等角”模型定义两个相等的角一边在同一直线上,另一边在该直线的同侧或异侧,第三个与之相等的角的顶点在前一组等角的顶点所确定的线段上或线段的延长线上,该角的两边分别位于一直线的同侧或异侧,并与两等角两边相交,就会形成一组相似三角形,习惯上把该组相似三角形称为“一线三等角型”相似三角形.二、“一线三等角”模型类型(1)点P在线段AB上,则有△ACP∽△BPD.①锐角一线三等角锐角一线三等角模型②直角一线三等角直角一线三等角模型③钝角一线三等角钝角一线三等角模型(2)点P在线段AB的延长线上,则有△ACP∽△BPD.①锐角一线三等角锐角一线三等角模型②直角一线三等角直角一线三等角模型③钝角一线三等角钝角一线三等角模型三、“一线三等角”模型常出现的题型1、等腰三角形中,在底边上作一角与底角相等;2、等腰梯形中上(下)底作一角与上(下)底角相等;3、矩形(正方形);4、矩形和正方形的翻折(简称:一线三直角);5、等边三角形的翻折;6、坐标系中的一线三直角包括已知相似比求点的坐标或直角三角形的讨论性问题.四、典例解析(一)一线三等角模型——等腰三角形【例题1】如图,已知:在Rt△ABC中,∠ACB=90°,AC=BC=4,点M是边AB的中点,点E、G分别是边AC、BC上的一点,∠EMG=45°,AC与MG的延长线相交于点F,(1)在不添加字母和线段的情况下写出图中一定相似的三角形,并证明其中的一对;(2)连接EG,当AE=3时,求EG的长.解析:(1)△AEM∽△BMG(一线三等角型);△FEM∽△FMA(共角共边型).(2)AE=3,CE=1,由△AEM∽△BMG可计算出BG=8/3,则CG=4/3.在Rt△CEG中,由勾股定理可得EG=5/3.另解:点M是AB的中点,恰好是“中点型一线三等角”,则有△AEM∽△BMG∽△MEG.对可解△AEM由余弦定理可计算出ME=√5,由△AEM∽△MEG,可得AE/ME=ME/EG,即3/√5=√5/EG,解得EG=5/3.(二)一线三等角模型——等腰梯形【例题2】已知在梯形ABCD中,AD∥BC,AD2,即y+2>2,∴y=-1/2x^2+5x/2-2>0,即15(舍去).五、小结1、此次课程展示了相似模型“一线三等角型”在初中数学范围内常见的两种考题形式;2、从压轴题中的复杂图形提炼出基本图形、快速灵活运用基本结论、反思、拓展提高,通过知识间的串联,找出一些通性通法,来提高解题效率.